Chứng minh rằng:Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên

Giải vở thực hành Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Bài 2 (9.21) trang 77 vở thực hành Toán lớp 7 Tập 2: Chứng minh rằng:

a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.

b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Lời giải:

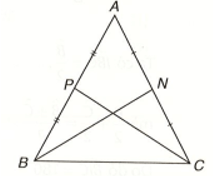
a) Tam giác ABC cân tại A và có BN, CP là hai đường trung tuyến. Ta cần chứng minh BN = CP.

Tam giác ABC cân tại A nên AB = AC; PBC^=NCB^.

Do N, P lần lượt là trung điểm của AC, AB nên BP = 12 AB, CN = 12 AC, do đó BP = CN.

Xét hai tam giác BCP và CBN, ta có:

BP = CN; PBC^=NCB^; BC chung, do đó ∆BCP = ∆CBN (c.g.c).

Suy ra CP = BN.

b) BN, CP là hai đường trung tuyến của tam giác ABC, BN = CP. Ta sẽ chứng minh AB = AC.

Gọi G là trọng tâm của tam giác ABC.

Xét hai tam giác PGB và NGC, ta có:

PG = NG; BG = CG; BGP^=CGN^ (đối đỉnh).

Vậy ∆PGB = ∆NGC (c.g.c), suy ra BP = NC.

Do đó AB = 2PB = 2NC = AC.

Vậy tam giác ABC cân tại A.

Xem thêm các bài giải vở thực hành Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

---