Công thức, cách tính diện tích xung quanh, diện tích toàn phần Hình hộp chữ nhật – Tổng hợp trên 200 Công thức, Định nghĩa, Định lí môn Toán giúp học sinh nắm vững kiến thức lý thuyết quan trọng, thường gặp để học tốt môn Toán hơn.-Công thức, cách tính diện tích xung quanh, diện tích toàn phần Hình hộp chữ nhật
Công thức, cách tính diện tích xung quanh, diện tích toàn phần Hình hộp chữ nhật
Công thức, cách tính diện tích xung quanh, diện tích toàn phần Hình hộp chữ nhật
1. Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
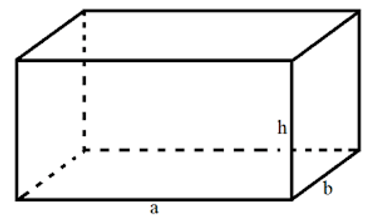
a) Định nghĩa
– Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
– Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.
b) Quy tắc
Giả sử hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là h.
– Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).
Sxq = (a + b) × 2 × h
– Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Stp = Sxq + Sđáy × 2 = (a + b) x 2 x h + 2 x a x b
Lưu ý:
– Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với 2.
– Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.
2. Một số dạng bài tập
Dạng 1: Tính diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật
Phương pháp: Áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.
Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.
Bài giải
Chu vi đáy của hình hộp chữ nhật là:
(8 + 6) × 2 = 28 (cm)
Diện tích xung quanh của hình hộp chữ nhật đó là:
28 × 4 = 112 (cm2)
Diện tích một đáy là:
8 × 6 = 48 (cm2)
Diện tích toàn phần của hình hộp chữ nhật đó là:
112 + 48 × 2 = 208(cm2)
Đáp số: Diện tích xung quanh: 112cm2
Diện tích toàn phần: 208cm2
Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật
Phương pháp:
*) Từ công thức Sxq = (a + b) x 2 x h:
– Tìm chiều cao theo công thức: h = Sxq : [(a + b) x 2] = Sxq: (a + b) : 2;
– Tìm tổng chu vi đáy theo công thức: (a + b) x 2 = Sxq : h.
*) Nếu biết diện tích toàn phần ta cũng thay vào công thức để tìm các đại lượng chưa biết.
Ví dụ. Cho hình hộp chữ nhật có diện tích xung quanh là 217,5m2 và nửa chu vi mặt đáy bằng 14,5m. Tính chiều cao của hình hộp chữ nhật đó.
Bài giải
Chu vi mặt đáy của hình hộp chữ nhật đó là:
14,5 × 2 = 29 (m)
Chiều cao của hình hộp chữ nhật đó là:
217,5 : 29 = 7,5 (m)
Đáp số: 7,5m
Dạng 3: Toán có lời văn (thường là tìm diện tích hộp, căn phòng, sơn tường …)
Phương pháp: Cần xác định xem diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần rồi áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.
Ví dụ. Một căn phòng dạng hình hộp chữ nhật có chiều dài 6m, chiều rộng 48dm, chiều cao 4m. Người ta muốn quét vôi các bức tường xung quanh và trần của căn phòng đó. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng 12m2 (biết rằng chỉ quét vôi bên trong phòng)?
Bài giải
Đổi 48dm = 4,8m
Diện tích xung quanh của căn phòng đó là:
(6 + 4,8) × 2 × 4 = 86,4 (m2)
Diện tích trần của căn phòng đó là:
6 × 4,8 = 28,8 (m2)
Diện tích cần quét vôi là:
86,4 + 28,8 – 12 = 103,2 (m2)
Đáp số: 103,2m2
3. Bài tập vận dụng
Bài 1. Một hình hộp chữ nhật có chiều dài 3,2dm, chiều rộng 0,5m và chiều cao 15cm. Tính diện tích xung quanh và diện tích toàn phần của hình hộp đó.
Bài 2. Một căn phòng hình hộp chữ nhật có chiều dài 9m, chiều rộng kém chiều dài 3m và chiều cao dài 4m. Người ta cần quét vôi tường và trần nhà trong căn phòng đó. Hỏi diện tích cần quét vôi là bao nhiêu, biết tổng diện tích các cửa và cửa sổ là 11,25m2?
Bài 3. Một cái thùng không nắp dạng hình hộp chữ nhật, chiều rộng bằng 3/5 chiều dài và kém chiều dài 1,2m, chiều cao dài 1,5m. Người ta sơn cả mặt trong và mặt ngoài của thùng, cứ 2m2 thì hết 0,5kg sơn. Tính lượng sơn đã sơn xong cái thùng đó.
Bài 4. Một cái thùng dạng hình hộp chữ nhật có chiều rộng 4dm, chiều cao 3,5dm và diện tích một đáy là 70dm2. Tính diện tích toàn phần của cái thùng đó.
Bài 5. Hải cần làm 2 cái thùng hình lập phương bằng sắt không có nắp cạnh 2,4m. Hỏi:
a) Hải phải cần bao nhiêu m2 sắt?
b) Hải tính sơn cả bên trong và bên ngoài 2 cái thùng đó thì phải mua bao nhiêu kg sơn, biết rằng cứ 20m2 thì cần 5kg sơn?
Bài 6. Hình hộp chữ nhật có diện tích đáy là 25,7dm2, diện tích xung quanh là 75,3dm2. Tính diện tích toàn phần của hình hộp chữ nhật đó.
Bài 7. Khoanh vào chữ cái đặt trước câu trả lời đúng. Một hình hộp chữ nhật có diện tích toàn phần là 25,27dm2, diện tích đáy là 625cm2. Hỏi diện tích xung quanh của hình hộp chữ nhật đó bằng bao nhiêu?
Bài 8. Cho một hộp giấy hình hộp chữ nhật có chiều dài là 1,2dm, chiều rộng là 5cm, chiều cao là 6cm. Tính diện tích toàn phần của hộp giấy đó.
Bài 9. Tính diện tích xung quanh và diện tích toàn phần của một hình hộp chữ nhất, biết chiều dài 12m6dm, chiều rộng bằng một nửa chiều dài, chiều cao 5m50cm.
Bài 10. Một phòng họp hình hộp chữ nhật có chiều dài là , chiều rộng kém chiều dài 20dm, chiều cao 35dm. Người ta muốn quét vôi trần nhà và bốn bức tường phía trong phòng. Biết rằng diện tích các cửa là 22,5m2. Tính diện tích cần quét vôi.
Xem thêm các bài viết về công thức, định nghĩa, tính chất môn Toán hay, chi tiết khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn