Công thức Định lý Py-ta-go và định lý Py-ta-go đảo hay, chi tiết – Toán lớp 7

---

---

Công thức Định lý Py-ta-go và định lý Py-ta-go đảo hay, chi tiết

Bài viết Công thức Định lý Py-ta-go và định lý Py-ta-go đảo hay, chi tiết Toán lớp 7 gồm 2 phần: Lý thuyết và Các ví dụ
áp dụng công thức trong bài có lời giải chi tiết giúp học sinh dễ học, dễ nhớ Công thức Định lý Py-ta-go và định lý Py-ta-go đảo hay, chi tiết.

I. Lý thuyết

1. Định lý Py – ta – go

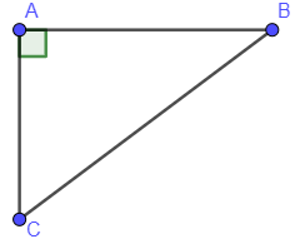
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương hai cạnh góc vuông.

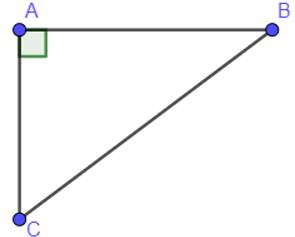
Tam giác ABC vuông tại A ta có: AB2+AC2=BC2

2. Định lý Py – ta – go đảo

Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.

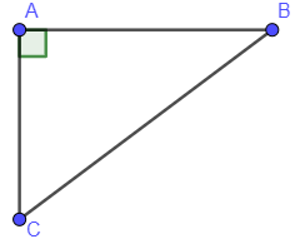
Xét tam giác ABC có: AB2+AC2=BC2 thì tam giác ABC vuông tại A.

II. Các ví dụ

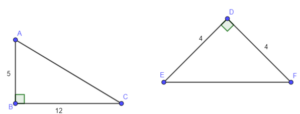
Ví dụ 1:  Tính độ dài AC, EF trong hình vẽ:

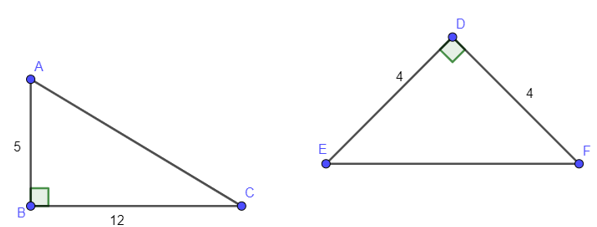
Lời giải:

+ Xét tam giác ABC vuông tại B ta có:

BC2+AB2=AC2 (định lý Py – ta – go)

122+52=AC2

AC2=144+25

AC2=169

⇒AC=13 (đơn vị độ dài)

+ Xét tam giác DEF vuông tại D ta có:

DE2+DF2=E​F2 (định lý Py – ta – go)

42+42=EF2

E​F2=16+16

EF2=32

⇒EF=32=42 (đơn vị độ dài)

Vậy AC = 13; EF=42

Ví dụ 2: Cho tam giác ABC vuông tại A có AB = 9cm, AC = 12cm. Tính BC.

Lời giải:

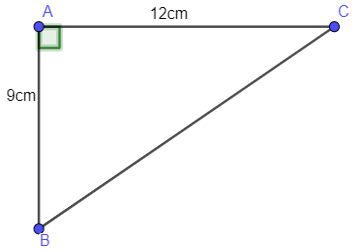
Áp dụng định lý Py – ta – go cho tam gác ABC vuông tại A ta có:

AB2+AC2=BC2

⇔92+122=BC2

⇔81+144=BC2

⇔BC2=225

⇔BC=15cm

Ví dụ 3: Cho tam giác ABC có: AB = 6 cm; AC = 8 cm; BC = 10 cm. Chứng minh BAC^=90°.

Lời giải:

Ta có:

AB2=62=36

AC2=82=64

BC2=102=100

AB2+AC2=36+64=100=BC2

⇒ΔABC vuông tại A (định lý Py – ta – go đảo)

⇒BAC^=90° (điều phải chứng minh)

Ví dụ 4: Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Gọi M là trung điểm của BC. Tính AM.

Lời giải:

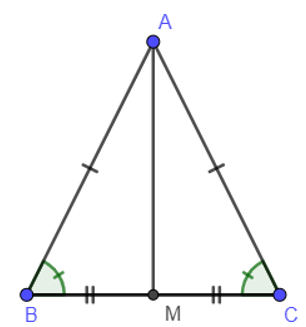
Vì ABC là tam giác cân ⇒AB=ACB^=C^ (tính chất)

Vì M là trung điểm của BC nên MB = MC

Xét tam giác ABM và tam giác ACM có:

AB = AC (chứng minh trên)

B^=C^ (chứng minh trên)

MB = MC (chứng minh trên)

Do đó ΔABM=ΔACM (c – g – c)

⇒AMB^=AMC^ (hai góc tương ứng) (1)

Lại có: AMB^+AMC^=180° (hai góc kề bù) (2)

Từ (1) và (2) ⇒AMB^=AMC^=90°

Xét tam giác ABM vuông tại M có:

AB2=AM2+MB2 (định lý Py – ta – go)

Mà AB = 10cm; MB=12BC=12.12=6cm nên

102=AM2+62

AM2=100−36

AM2=64

AM = 8cm

Vậy AM = 8cm.

Xem thêm các Công thức Toán lớp 7 quan trọng hay khác:

---

---

---