Công thức Tổng các góc trong một tam giác lớp 7 (hay, chi tiết)

Bài viết Công thức Tổng các góc trong một tam giác trình bày đầy đủ công thức, ví dụ minh họa có lời giải chi tiết và các bài tập tự luyện giúp học sinh
nắm vững kiến thức trọng tâm về Tổng các góc trong một tam giác từ đó học tốt môn Toán.

Công thức Tổng các góc trong một tam giác lớp 7 (hay, chi tiết)

1. Công thức

a) Định lí tổng ba góc trong một tam giác

Cho tam giác ABC.

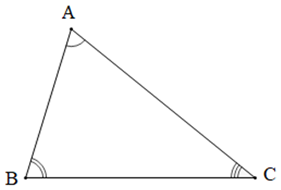
Khi đó, theo định lí tổng ba góc của một tam giác, ta có:

A^+B^+C^=180°.

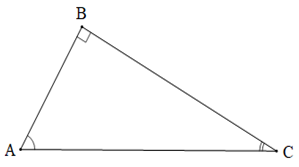
b) Áp dụng vào tam giác vuông

Cho tam giác ABC vuông tại B.

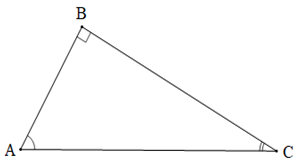
Khi đó,theo định lí tổng ba góc của một tam giác, ta có: A^+C^=90° .

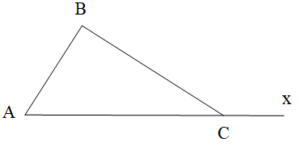
c) Góc ngoài của tam giác

Cho tam giác ABC có BCx^ là góc ngoài tại đỉnh C của tam giác ABC.

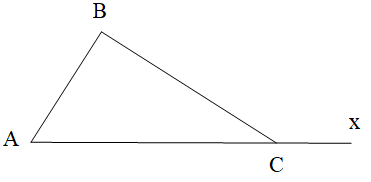
Khi đó, theo tính chất góc ngoài tam giác, ta có: BCx^=A^+B^ .

2. Ví dụ minh họa:

Ví dụ 1. Tìmsố đo của góc xtrong các hình vẽ dưới đây:

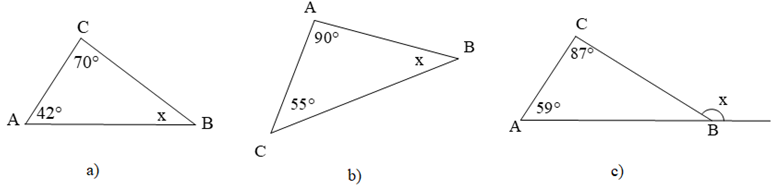
Hướng dẫn giải:

a)

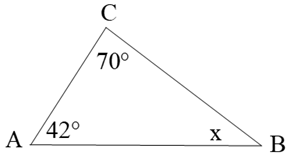
Xét tam giác ABC, ta có:

A^+B^+C^=180° (Tổng ba góc trong tam giác bằng 180°)

Suy ra x=B^=180°−A^−B^=180°−42°−70°=68° .

Vậy x = 68°.

b)

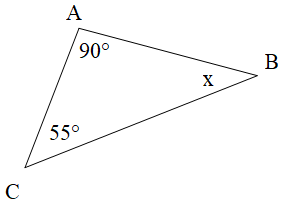
Tam giác ABC có A^=90° nên là ∆ABC vuông tại A.

Xét ∆ABC vuông tại A, ta có:

B^+C^=90° (trong tam giác vuông hai góc nhọn phụ nhau)

Suy ra x=B^=90°−C^=90°−55°=35° .

Vậy x = 35°.

c)

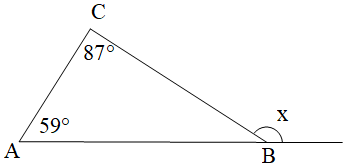
Ta có góc x là góc ngoài của ∆ABC tại đỉnh B nên ta có:

x=A^+C^ (tính chất góc ngoài của một tam giác)

x = 59° + 87° = 146°.

Vậy x = 146°.

Ví dụ 2. Tìmsố đo của các góc x, y trong hình vẽ dưới đây:

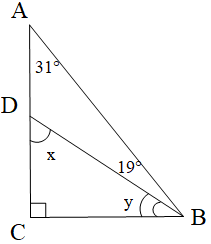
Hướng dẫn giải:

+) Tính số đo góc x

Cách 1:

Xét tam giác ADB, ta có:

ADB^+DAB^+ABD^=180°(tổng ba góc trong tam giác bằng 180^o)

ADB^=180°−DAB^+ABD^

ADB^=180°−31°+19°=180°−50°=130°

Mà ADB^+BDC^=180°(hai góc kề bù)

Suy ra x=BDC^=180°−ADC^=180°−130°=50°

Cách 2:

Ta có x=BDC^ là góc ngoài của tam giác tại đỉnh D của ∆ABD nên:

x=BDC^=DAB^+ABD^

Hay x = 31° + 19° = 50°

Vậy x = 50°.

+) Tính số đo góc y:

Xét tam giác DCB có BCD^=90° nên tam giác DCB vuông tại C

Suy ra DBC^+BDC^=90° (trong tam giác vuông hai góc nhọn phụ nhau)

Do đó y=90°−BDC^=90°−50°=40°

Vậy x = 50^o và y = 40^o.

3. Bài tập tự luyện

Bài 1. Cho hình vẽ bên dưới.

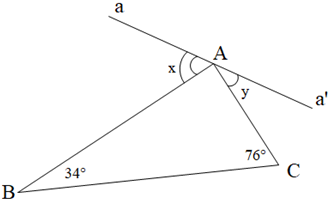
a) Tính số đo góc BAC.

b) Tính giá trị x + y.

Bài 2. Cho hình thang cân ABCD như hình vẽ.

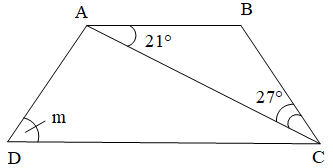
a) Tính số đo góc ACD.

b) Tính số đo góc m.

Bài 3. Cho hình thoi ABCD như hình vẽ.

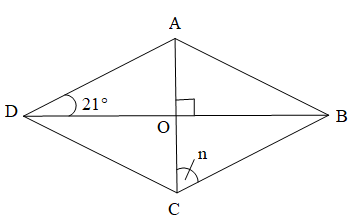
a) Tính số đo góc COB.

b) So sánh số đo góc OBC và số đo góc n.

Bài 4. Cho hình bình hành ABCD như hình vẽ.

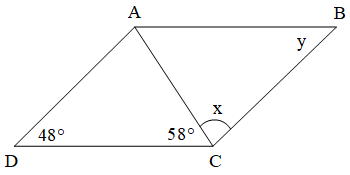
a) Tính số đo góc DAC.

b) So sánh số đo x và y.

c) Tính giá trị x – y.

Bài 5. Cho tam giác ABC như hình vẽ, biết AI là tia phân giác góc CAB.

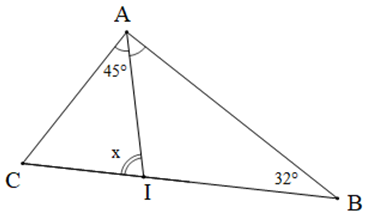
a) Tam giác ABC là tam giác gì?

b) So sánh số đo hai góc ACI^ và AIB^.

c) Tính số đo x.

Xem thêm các bài viết về công thức Toán hay, chi tiết khác:

---