Công thức về hai góc kề nhau, bù nhau và kề bù lớp 7 (hay, chi tiết)

Bài viết Công thức về hai góc kề nhau, bù nhau và kề bù trình bày đầy đủ công thức, ví dụ minh họa có lời giải chi tiết và các bài tập tự luyện giúp học sinh
nắm vững kiến thức trọng tâm về Công thức về hai góc kề nhau, bù nhau và kề bù từ đó học tốt môn Toán.

Công thức về hai góc kề nhau, bù nhau và kề bù lớp 7 (hay, chi tiết)

1. Công thức

a) Hai góc kề nhau

Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía đối với đường thẳng chứa cạnh chung đó.

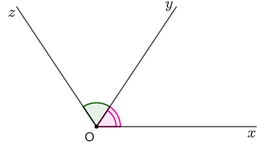
xOy^ và yOz^kề nhau thì tia Oy là tia nằm giữa hai tia Ox và Oz, khi đó:

xOy^ và yOz^kề nhau thì xOy^+yOz^=xOz^.

b) Hai góc bù nhau

Hai góc bù nhau là hai góc có tổng số đo bằng 180°.

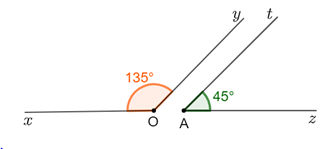
xOy^ và zAt^bù nhau thì: xOy^+zAt^=180°.

c) Hai góc kề bù

Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

Hai góc kề bù còn được hiểu là hai góc vừa kề nhau, vừa bù nhau.

xOy^ và yOz^kề bù thì tia Oy nằm giữa hai tia Ox, Oz và xOy^+yOz^=180°

2. Ví dụ minh hoạ

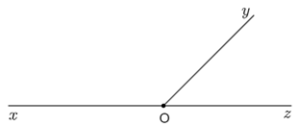
Ví dụ 1. Tìm các cặp góc kề bù ở hình vẽ dưới đây biết xOz^=180°.

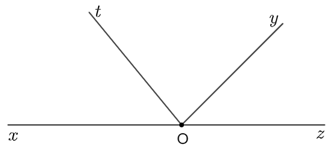
Hướng dẫn giải:

+) Tia Oy nằm giữa hai tia Ox, Oz nên xOy^+yOz^=xOz^

Mà xOz^=180° suy ra xOy^+yOz^=180°

Do đó hai góc xOy^và yOz^là hai góc kề bù.

+) Tia Ot nằm giữa hai tia Ox, Oz nên xOt^+tOz^=xOz^

Mà xOz^=180° suy ra xOt^+tOz^=180°

Do đó hai góc xOt^và tOz^là hai góc kề bù.

Ví dụ 2. Hai góc xOy^và yOz^là hai góc kề bù, biết yOz^=75°. Tính số đo góc xOy^.

Hướng dẫn giải:

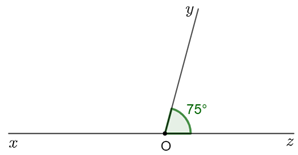
Hai góc xOy^và yOz^kề bù nên xOy^+yOz^=180°(tính chất hai góc kề bù)

Hay xOy^+75°=180°

Khi đó xOy^=180°−75°

Do đó xOy^=105°.

Vậy xOy^=105°.

Ví dụ 3. Cho tia OB nằm giữa hai tia OA và OC, biết AOB^=30°; AOC^=135°.

a) Tính số đo góc BOC^.

b) Vẽ tia OD là tia đối của tia OB. Tính số đo góc COD^.

Hướng dẫn giải

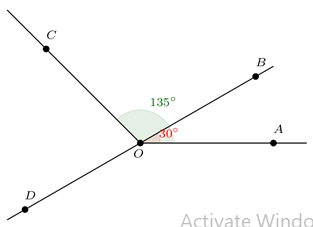
a) Tia OBnằm giữa hai tia OA và OC nên AOB^+BOC^=AOC^

Hay 30°+BOC^=135°

Suy ra BOC^=135°−30°

Do đó BOC^=105°

Vậy BOC^=105°.

b) OD là tia đối của tia OB nên hai góc BOC^và COD^là hai góc kề bù.

Do đó: BOC^+COD^=180°(tính chất hai góc kề bù)

Hay 105°+COD^=180°

Suy ra COD^=180°−105°

Do đó COD^=75°

Vậy COD^=75°.

3. Bài tập tự luyện

Bài 1. Cho hình dưới đây, kể tên các cặp góc kề bù. Tính số đo các cặp góc kề bù đó.

Bài 2. Hai đường thẳng AB và CD cắt nhau tại O, biết BOD^=50°. Tính số đo các góc AOD^,AOC^,BOC^.

Bài 3. Cho tia OB nằm giữa hai tia OA và OC, biết AOB^=20°;AOC^=125°.

a) Tính số đo góc BOC^.

b) Vẽ tia OD là tia đối của tia OB. Tính số đo các góc COD^.

Bài 4. Cho xOy^và yOz^là hai góc kề nhau, biết xOy^=75°; yOz^=30°.

a) Tính số đo góc xOz^.

b) Gọi Ot là tia đối của tia Oy. Tính số đo góc xOt^.

Bài 5. Tia OB nằm giữa hai tia OA và OC, biết AOC^=80°và BOC^=13AOB^.

a) Tính số đo góc BOC^và AOB^.

b) Vẽ góc AOD^=100°là góc kề với góc AOC^. Chứng tỏ rằng AOC^và AOD^là hai kề bù.

Xem thêm các bài viết về công thức Toán hay, chi tiết khác:

---