Công thức xác định đường tiệm cận của đồ thị hàm số – Toán lớp 12

Công thức xác định đường tiệm cận của đồ thị hàm số Toán 12 sẽ giúp học sinh lớp 12 nắm vững công thức, biết cách làm bài tập
từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.

Công thức xác định đường tiệm cận của đồ thị hàm số – Toán lớp 12

1. Công thức

a) Đường tiệm cận ngang

Đường thẳng y = y₀ được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu:

limx→+∞fx=y0 hoặc limx→−∞fx=y0.

b) Đường tiệm cận đứng

Đường thẳng x = x₀ được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

c) Đường tiệm cận xiên

Đường thẳng y = ax + b (a ≠ 0) được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu:

limx→+∞fx−ax+b=0 hoặc limx→−∞fx−ax+b=0.

→ Để xác định hệ số a, b của đường tiệm cận xiên y = ax + b của đồ thị hàm số y = f(x), ta có thể áp dụng công thức sau:

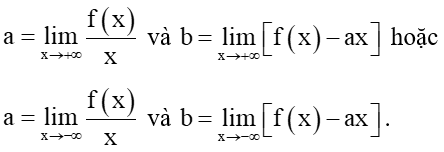
Chú ý: Hàm phân thức y=ax+bcx+d có TCN là y=ac và TCĐ là x=−dc.

2. Ví dụ minh họa

Ví dụ 1. Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị mỗi hàm số sau:

a) y=x+1x−2;                                                  

b) y=3−2x3x+1.

Lời giải

a) TXĐ: D = ℝ {2}.

Ta có: limx→±∞x+1x−2=1 nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số đã cho.

Do limx→2+x+1x−2=+∞; limx→2−x+1x−2=−∞ nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số đã cho.

b) TXĐ: D = ℝ −13.

Vì limx→±∞3−2x3x+1=−23 nên đường thẳng y=−23 là tiệm cận ngang của đồ thị hàm số đã cho.

Vì limx→−13+3−2x3x+1=+∞; limx→−13−3−2x3x+1=−∞ nên đường thẳng x=−13 là tiệm cận đứng của đồ thị hàm số đã cho.

Ví dụ 2. Tìm các tiệm cận đứng và tiệm cận ngang (nếu có) của đồ thị mỗi hàm số sau:

a) y=x2−12x+27×2−4x+5;                           

b) y=2−xx2−4x+3.

Lời giải

a) TXĐ: D = ℝ, do đó đồ thị hàm số không có tiệm cận đứng.

Vì limx→±∞x2−12x+27×2−4x+5=1 nên đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số đã cho.

b) TXĐ: D = ℝ {1; 3}.

Vì limx→±∞2−xx2−4x+3=0 nên đường thẳng y = 0  là tiệm cận ngang của đồ thị hàm số đã cho.

Vì limx→1−2−xx2−4x+3=+∞ nên x = 1 là một đường tiệm cận đứng của đồ thị hàm số đã cho.

Vì limx→3+2−xx2−4x+3=−∞ nên x = 3 là một đường tiệm cận đứng của đồ thị hàm số đã cho.

Vậy đồ thị hàm số có TCN là y = 0; TCĐ là x = 1 và x = 3.

Ví dụ 3. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau:

a) y=2×2−3x+2x−1;

b) y=x−3+1×2.

Lời giải

a) y=2×2−3x+2x−1

Hàm số đã cho có tập xác định là ℝ {1}.

Ta có limx→1−2×2−3x+2x−1=−∞; limx→1+2×2−3x+2x−1=+∞. Do đó đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số đã cho.

a=limx→+∞yx=limx→+∞2×2−3x+2x−1x=2;

b=limx→+∞y−2x=limx→+∞2×2−3x+2x−1−2x=limx→+∞−x+2x−1=−1.

Do đó, đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho.

b) y=x−3+1×2

Hàm số đã cho có tập xác định là ℝ {0}.

Ta có limx→0−x−3+1×2=+∞; limx→0+x−3+1×2=+∞. Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số đã cho.

Ta cũng có limx→+∞y−x−3=limx→+∞1×2=0; limx→−∞y−x−3=limx→−∞1×2=0. Do đó, đường thẳng y = x – 3 là tiệm cận xiên của đồ thị hàm số đã cho.

3. Bài tập tự luyện

Bài 1. Tìm các đường tiệm cận đứng, tiệm cận ngang của đồ thị mỗi hàm số sau:

a) y=x3−x;                              

b) y=2x+33−2x;                 

c) y=5x+5−2.

Bài 2. Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị mỗi hàm số sau:

a) y=x2+3xx2−4;               

b) y=x2−3x+2×2−4x+5;          

c) y=x+2x−2.

Bài 3. Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:

a) y=4x+5×2−4;

b) y=−x2+63×2+7;

c) y=2×2+3×1−x.

Bài 4. Đồ thị hàm số y=xx2−3x−4+x có bao nhiêu đường tiệm cận?

Bài 5. Tìm m để đồ thị hàm số y=x2−mx+2×2−1 có đúng 2 đường tiệm cận.

Bài 6. Tổng chi phí để sản xuất x sản phẩm của một nhà máy được tính theo công thức

T = 30x + 200 000 (nghìn đồng).

a) Viết công thức tính chi phí trung bình C(x) của 1 sản phẩm khi sản xuất được x sản phẩm.

b) Xem y = C(x) là một hàm số xác định trên khoảng (0; +∞), hãy tìm tiệm cận ngang của đồ thị hàm số đã cho.

c) Nêu nhận xét về chi phí để tạo ra 1 sản phẩm khi x càng lớn.

Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:

---