Công thức xác định số trung bình cộng của mẫu số liệu ghép nhóm lớp 11 (hay, chi tiết)

Bài viết Công thức xác định số trung bình cộng của mẫu số liệu ghép nhóm trình bày đầy đủ công thức, ví dụ minh họa có lời giải chi tiết và các bài tập tự luyện giúp học sinh lớp 11
nắm vững kiến thức trọng tâm về Công thức xác định số trung bình cộng của mẫu số liệu ghép nhóm từ đó học tốt môn Toán.

Công thức xác định số trung bình cộng của mẫu số liệu ghép nhóm lớp 11 (hay, chi tiết)

1. Công thức

Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu được tính theo công thức:

x¯=n1x1+ n2x2+…+ nmxmn

Trong đó:

+) x_1, x₂, …, x_m là giá trị đại diện của nhóm 1, nhóm 2, …., nhóm m.

+) n_1, n₂, …, n_m là tần số tương ứng của các nhóm.

+) n = n₁ + n₂ + …. + n_m.

2. Ví dụ minh họa

Ví dụ 1. Một cửa hàng bán truyện tranh thống kê số lượng truyện được bán mỗi ngày trong ba tháng ở bảng sau:

Hãy tính số trung bình cộng của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải:

Ta có bảng thống kê số truyện tranh được bán mỗi ngày theo giá trị đại diện:

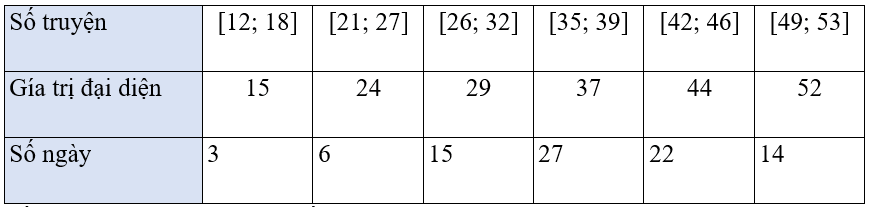
Số trung bình cộng của mẫu số liệu ghép nhóm trên là:

x¯=15⋅3 + 24⋅6 + 29⋅15 + 37⋅27 + 44⋅22 + 52⋅1487≈38,15

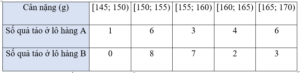
Ví dụ 2. Kết quả khảo sát cân nặng của 20 quả táo ở mỗi lô hàng A và B được cho ở bảng sau:

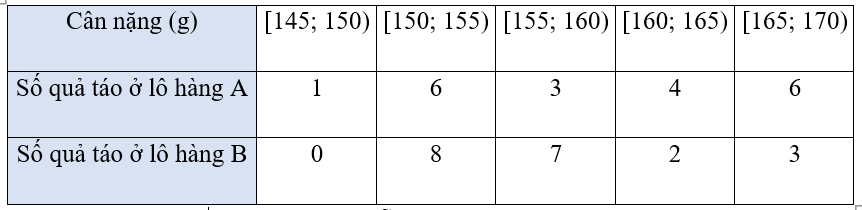
Hãy so sánh cân nặng trung bình của mỗi quả táo ở lô hàng A với lô hàng B.

Hướng dẫn giải:

Ta có bảng thống kê số lượng cam theo giá trị đại diện:

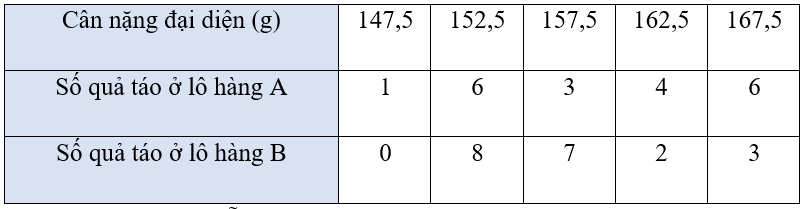
Cân nặng trung bình của mỗi quả táo ở lô hàng A là:

147,5⋅1+152,5⋅6+157,5⋅3+162,5⋅4+167,5⋅620=159,5(g).

Cân nặng trung bình của mỗi quả táo ở lô hàng B là:

147,5⋅0+152,5⋅8+157,5⋅7+162,5⋅2+167,5⋅320=157,5(g).

Vì 159, 5 > 157, 5 nên cân nặng trung bình của một quả táo ở lô A lớn hơn ở lô B.

3. Bài tập tự luyện

Bài 1. Tìm chiều cao trung bình của học sinh lớp 11A được cho bởi bảng sau:

Chiều cao	[140; 150)	[150; 160)	[160; 170)	[170; 180)	[180; 190)
Số học sinh	2	4	25	6	1

Bài 2. Khảo sát thời gian chơi game của một số học sinh trong tuần trước được kết quả như sau:

Thời gian (phút)	[10; 15)	[15; 20)	[20; 25)	[25; 30)	[30; 35)
Số học sinh	8	16	4	2	2

Tìm thời gian chơi game trung bình trong tuần trước của các bạn học sinh này.

Bài 3. Cho mẫu số liệu ghép nhóm như sau:

Nhóm	[3; 7)	[7; 11)	[11; 15)	[15; 19)	[19; 23)	[23; 27)
Tần số	3	2	24	16	4	1

Tìm số trung bình cộng của mẫu số liệu ghép nhóm trên.

Bài 4. Cho mẫu số liệu ghép nhóm như sau:

Nhóm	[0; 10)	[10; 20)	[20; 30)	[30; 40)	[40; 50)
Tần số	6	x	14	10	2

Tìm giá trị x biết số trung bình cộng của mẫu số liệu trên là 24,5.

Bài 5. Cho mẫu số liệu ghép nhóm về thời gian đi từ nhà đến trường của các học sinh lớp 11A như sau:

Thời gian	[5; 10)	[10; 15)	[15; 20)	[20; 30)
Số học sinh	5	x	8	7

Hãy tìm số học sinh đi học trong khoảng [10; 15) biết số trung bình cộng của mẫu số liệu trên là 17,75.

Xem thêm các bài viết về công thức Toán hay, chi tiết khác:

---