Đồ thị hàm số y= ax + b (a ≠ 0) | Chuyên đề Toán 9 – Tuyển tập chuyên đề Toán 9 chọn lọc với đầy đủ phương pháp giải, bài tập tự luận, trắc nghiệm giúp bạn học tốt môn Toán 9.-Đồ thị hàm số y= ax + b (a ≠ 0)
Đồ thị hàm số y= ax + b (a ≠ 0)
Cách giải Đồ thị hàm số y= ax + b (a ≠ 0) lớp 9 với phương pháp giải chi tiết và bài tập đa dạng giúp học sinh
ôn tập, biết cách làm bài tập Đồ thị hàm số y= ax + b (a ≠ 0).
Đồ thị hàm số y= ax + b (a ≠ 0)
A. Phương pháp giải
Phương pháp
1, Đường thẳng y=ax+b có hệ số góc là a.
2, Hai đường thẳng song song thì có hệ số góc bằng nhau
3, Hai đường thẳng vuông góc thì có tích hệ số góc bằng -1
4, Đường thẳng y=ax+b(a > 0) tạo với tia Ox một góc thì
5, Cách vẽ đồ thị hàm số y=ax+b ( a ≠ 0).
1, Xét trường hợp b=0
Khi b=0 thì y=a.x. Đồ thị của hàm số y= ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).
2, Xét trường hợp y=ax+b với
Bước 1: Cho x=0 thì y=b, ta được điểm P(0;b) thuộc trục Oy.
Cho y= 0 thì x= -b/a , ta được điểm Q(-b/a;0) thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y=ax+b.
B. Bài tập tự luận
Bài 1: Vẽ đồ thị hàm số của các hàm số
a, y= 2x
b, y=-3x+3
Hướng dẫn giải
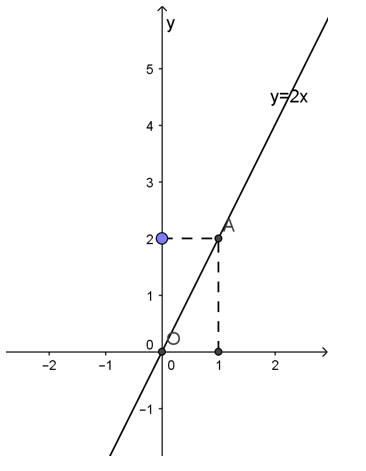
a, y=2x
Đồ thị hàm số y=2x đi qua điểm O(0; 0) và điểm A(1; 2)
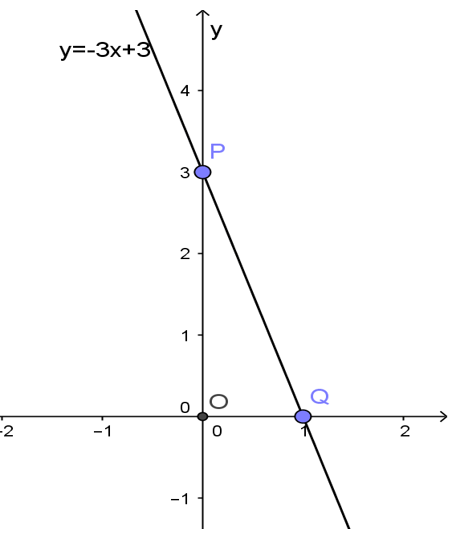
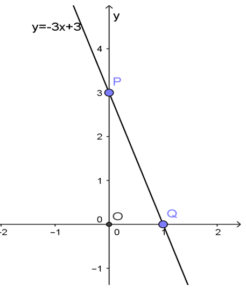
b, y=-3x+3
Cho x=0 thì y=3, ta được điểm P(0; 3) thuộc trục tung Oy
Cho y=0 thì x=1, ta được điểm Q(1; 0) thuộc trục hoành Ox
Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y=-3x+3
Bài 2: a, Cho đồ thị hàm số y=ax+7 đi qua M(2; 11). Tìm a
b, Biết rằng khi x=3 thì hàm số y=2x+b có giá trị bằng 8, tìm b
c, Cho hàm số y=(m+1)x. Xác định m để đồ thị hàm số đi qua A(1; 2)
Hướng dẫn giải
a, Vì đồ thị hàm số y=ax+7 (1) đi qua M(2; 11) nên thay x=2; y=11 vào (1) ta được:11=2a+7. Từ đó suy ra a=2.
Vậy a=2
b, Thay y=8; x=3 vào hàm số y=2x+b ta được: 8=6+b. Suy ra b=2
Vậy b=2
c, Vì đồ thị hàm số y=(m+1)x (2) đi qua A(1; 2) nên thay x=1; y=2 vào (2) ta được: 2=(m+1).1. Từ đó suy ra m=1
Vậy m=1
Bài 3: Xác định hàm số y=ax+b trong mỗi trường hợp sau, biết đồ thị của hàm số là đường thẳng đi qua gốc tọa độ và:
a, Đi qua điểm A(3;2)
b, Có hệ số a= √3
c, Song song với đường thẳng y=3x+1
Hướng dẫn giải
Nhắc lại: Đồ thị hàm số đi qua gốc tọa độ O(0;0) có dạng y=ax (a ≠0)
a, Vì đồ thị hàm số y=ax+b (a ≠ 0) đi qua gốc tọa độ O(0;0) nên có dạng y=ax (a ≠ 0)
Vì đồ thị hàm số đi qua điểm A(3;2) nên ta có: 2=3.a ⇔ a = 2/3
Vậy hàm số cần tìm là y = 2/3x
b, Vì đồ thị hàm số y=ax+b (a ≠ 0) đi qua gốc tọa độ O(0;0) nên có dạng y=ax(a ≠ 0)
Vì hàm số đã cho có hệ số góc là a= √3 nên hàm số cần tìm là y= √3x
c, Vì đồ thị hàm số y=ax+b (a ≠ 0) đi qua gốc tọa độ O(0;0) nên có dạng y=ax( a ≠ 0)
Vì đồ thị hàm số y=ax (a ≠ 0) song song với đường thẳng y=3x+1 nên a=3.
Vậy hàm số cần tìm là y=3x.
Bài 4: Cho đường thẳng y=(k+1)x+k. (1)
a, Tìm giá trị của k để đường thẳng (1) đi qua gốc tọa độ.
b, Tìm giá trị của k để đường thẳng (1) cắt trục tung tại điểm có tung độ bằng 2.
c, Tìm giá trị của k để đường thẳng (1) song song với đường thẳng y=5x-5.
Hướng dẫn giải
a, Đường thẳng y=ax+b đi qua gốc tọa độ khi b=0, nên đường thẳng y=(k+1)x+k qua gốc tọa độ khi k=0, khi đó hàm số là y=x.
b, Đường thẳng y=ax+b cắt trục tung tại điểm có tung độ bằng b. Do đó, đường thẳng y=(k+1)x+k cắt trục tung tại điểm có tung độ bằng 2 khi k=2.
Vậy k=2 và đường thẳng cần tìm là y=3x+2
c, Đường thẳng y=(k+1)x+k song song với đường thẳng y=5x-5 khi và chỉ khi k+1=5 và. Từ đó suy ra k=4.
Vậy hàm số cần tìm là y=5x+4.
Bài 5: a, Vẽ đồ thị của các hàm số y=x+1 và y=-x+3 trên cùng một mặt phẳng tọa độ.
b, Hai đường thẳng y=x+1 và y=-x+3 cắt nhau tại C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ của các điểm A, B, C.
c, Tính chu vi và diện tích tam giác ABC.
Hướng dẫn giải
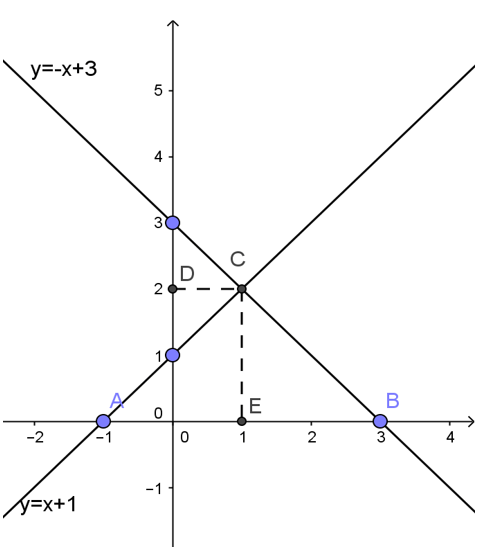
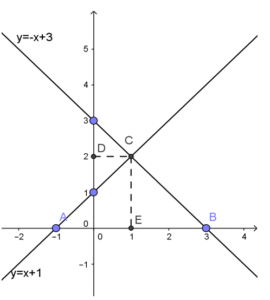
a, Đồ thị hàm số y=x+1 đi qua A(-1; 0) và (0; 1)
Đồ thị hàm số y=-x+3 đi qua B(3; 0) và (0; 3)
b, Với đường thẳng y=x+1:
Cho y=0 ta suy ra x=-1. Vì vậy, đường thẳng cắt trục Ox tại A(-1; 0)
Với đường thẳng y=-x+3:
Cho y=0 ta tuy ra x=3. Vì vậy, đường thẳng cắt trục Ox tại B(3; 0)
Gọi C (x; y) là giao điểm của đường thẳng y=x+1 và đường thẳng y=-x+3.
Vì C(x; y) thuộc vào cả 2 đường thẳng trên nên ta có: x+1=-x+3. Từ đó suy ra x=1
Thay x=1 vào hàm y=x+1 ta được y=2
Vậy C(1; 2)
C. Bài tập tự luyện
Bài 1. Cho hai hàm số y = x và y = 3x + 3
a) Vẽ đồ thị các hàm số trên trên cùng một hệ trục tọa độ;
b) Tìm tọa độ giao điểm M của hai đồ thị trên.
Bài 2. Cho hàm số y = (m + 5)x – m.
a) Đồ thị hàm số đi qua điểm A(– 2; – 2). Tìm m;
b) Xác định giá trị của tham số m để đồ thị hàm số:
Cắt trục hoành tại điểm có hoành độ bằng 3.
Cắt trục tung tại điểm có tung độ bằng – 4.
c) Vẽ đồ thị của hai hàm số tương ứng với các giá trị của m tìm được ở trên trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đồ thị vừa vẽ được
Bài 3. Cho hàm số y = 2x + 1 có đồ thị là d1 và y = 3 – x có đồ thị là d2.
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ;
b) Hai đường thẳng d1 và d2 cắt nhau tại C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ của các điểm A, B, C;
c) Tính chu vi và diện tích của tam giác ABC.
Bài 4. Với giá trị nào của m thì đồ thị hàm số y = 4x + m + 2 và y = 1 – 2x – 5 – 2m cắt nhau tại một điểm trên trục tung?
Bài 5. Cho ba đường thẳng d1: y = 2x + 1; d2: y = x + 3; d3: y = 3x – 1
a) Vẽ đồ thị của ba đường thẳng trên cùng một hệ trục tọa độ;
b) Gọi A là giao điểm của hai đường thẳng d1 và d3. Tìm tọa độ giao điểm A;
c) Chứng minh ba đường thẳng trên đồng quy;
d) Với giá trị nào của điểm m thì đường thẳng y = (m – 1)x + m cũng đi qua giao điểm của tất cả các đường thẳng đó?
Tham khảo thêm các Chuyên đề Toán lớp 9 khác:
Mục lục các Chuyên đề Toán lớp 9:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn