Đường tiệm cận của đồ thị hàm số (Lý thuyết Toán lớp 12) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Đường tiệm cận của đồ thị hàm số (Lý thuyết Toán lớp 12) | Kết nối tri thức

Lý thuyết Đường tiệm cận của đồ thị hàm số

1. Đường tiệm cận ngang

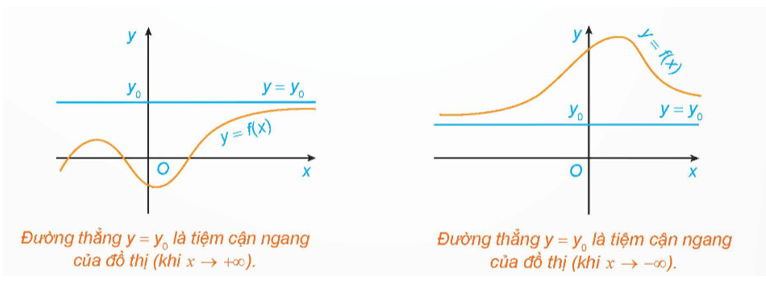
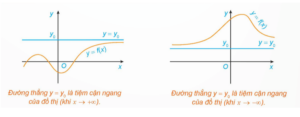
Đường thẳng y = y₀ gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu limx→+∞f⁢(x)=y0 hoặc limx→-∞f⁢(x)=y0.

Ví dụ 1. Tìm tiệm cận ngang của đồ thị hàm số y=2x−1 .

Hướng dẫn giải

Ta có limx→+∞y=limx→+∞2x−1=0 ; limx→−∞y=limx→−∞2x−1=0 .

Vậy y = 0 là tiệm cận ngang của đồ thị hàm số.

2. Đường tiệm cận đứng

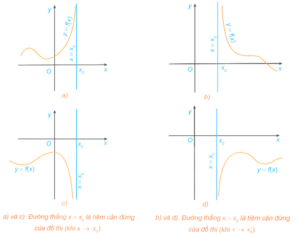
Đường thẳng x = x₀ gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

limx→x0+fx=+∞;limx→x0−fx=−∞;limx→x0+fx=−∞;limx→x0−fx=+∞

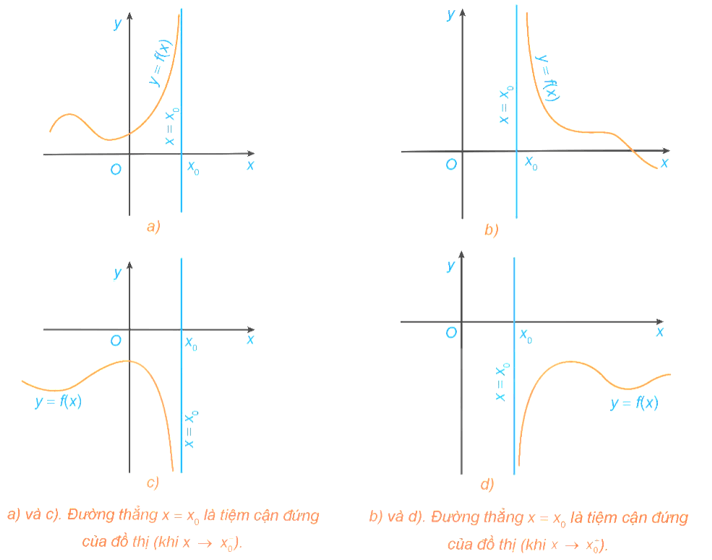
Ví dụ 2. Tìm tiệm cận đứng của đồ thị hàm số y=3x+6x−2 .

Hướng dẫn giải

Ta có limx→2+y=limx→2+3x+6x−2=+∞;limx→2−y=limx→2−3x+6x−2=−∞ .

Do đó đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

3. Đường tiệm cận xiên

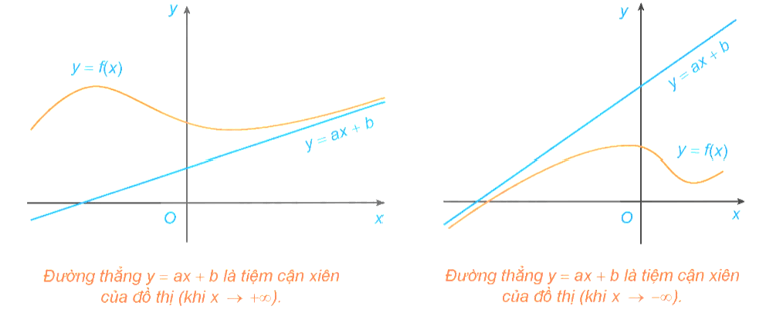
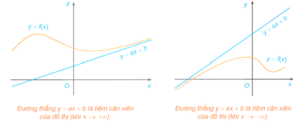
Đường thẳng y = ax + b (a ≠ 0) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu limx→+∞fx−ax+b=0 hoặc limx→−∞fx−ax+b=0.

Ví dụ 3. Tìm tiệm cận xiên của đồ thị hàm số y=fx=2x+1−1x+2 .

Hướng dẫn giải

Ta có limx→+∞fx−2x+1=limx→+∞−1x+2=0 ;

limx→−∞fx−2x+1=limx→−∞−1x+2=0.

Do đó y = 2x + 1 là tiệm cận xiên của đồ thị hàm số.

Chú ý:

Ta biết rằng nếu đường thẳng y = ax + b (a ≠ 0) là tiệm cận xiên của đồ thị hàm số y = f(x) thì limx→+∞fx−ax+b=0  hoặc limx→−∞fx−ax+b=0.

Do đó limx→+∞[f⁢(x)-(a⁢x+b)].1x=0 hoặc limx→-∞[f⁢(x)-(a⁢x+b)].1x=0.

Từ đây suy ra a=limx→+∞fxx hoặc a=limx→−∞fxx.

Khi đó, ta có b=limx→+∞fx−ax hoặc b=limx→−∞fx−ax.

Ngược lại, với a và b xác định như trên, đường thẳng y = ax + b (a ≠ 0) là một tiệm cận xiên của đồ thị hàm số y = f(x). Đặc biệt, nếu a = 0 thì đồ thị hàm số có tiệm cận ngang.

Ví dụ 4. Tìm tiệm cận xiên của đồ thị hàm số y=fx=x2−2xx+1 .

Hướng dẫn giải

Ta có a=limx→+∞fxx=limx→+∞x2−2xx2+x=1; b=limx→+∞fx−x=limx→+∞−3xx+1=−3.

Tương tự limx→−∞fxx=1; limx→−∞fx−x=−3.

Vậy đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = x – 3.

Nhận xét:

Trong thực hành, để tìm tiệm cận xiên của hàm phân thức trong ví dụ 4, ta viết:

y=fx=x2−2xx+1=x−3+3x+1.

Ta có limx→+∞fx−x−3=limx→+∞3x+1=0; limx→−∞fx−x−3=limx→−∞3x+1=0.

Vậy đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = x – 3.

Bài tập Đường tiệm cận của đồ thị hàm số

Bài 1. Đồ thị hàm số y=1−3xx+2 có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

A. x = −2 và y = −3.                                      B. x = −2 và y = 1.

C. x = −2 và y = 3.                                        D. x = 2 và y = 1.

Hướng dẫn giải

Đáp án đúng là: A

Có limx→−2+y=limx→−2+1−3xx+2=+∞;limx→−2−y=limx→−2−1−3xx+2=−∞

Do đó x = −2 là tiệm cận đứng của đồ thị hàm số.

Có limx→+∞y=limx→+∞1−3xx+2=−3;limx→−∞y=limx→−∞1−3xx+2=−3.

Do đó y = −3 là tiệm cận ngang của đồ thị hàm số.

Bài 2. Cho hàm số y = f(x) có bảng biến thiên như sau

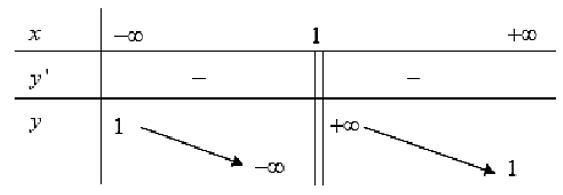
Trong các mệnh đề sau về hàm số y = f(x), mệnh đề nào đúng?

A. Đồ thị hàm số có tiệm cận đứng x = 1.

B. Hàm số nghịch biến trên ℝ.

C. Hàm số đồng biến trên ℝ.

D. Hàm số có một điểm cực trị.

Hướng dẫn giải

Đáp án đúng là: A

Dựa vào bảng biến thiên, ta có:

+) Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).

+) Hàm số không có cực trị

+) Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số và đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Bài 3. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=2x+1x+1.

Hướng dẫn giải

Tập xác định: D = ℝ{−1}.

limx→−1−y=limx→−1−2x+1x+1=+∞;limx→−1+y=limx→−1+2x+1x+1=−∞

Do đó đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

limx→+∞y=limx→+∞2x+1x+1=2;limx→−∞y=limx→−∞2x+1x+1=2.

Do đó đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

Bài 4. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số y=x2+x+1x+1.

Hướng dẫn giải

Tập xác định: D = ℝ{−1}.

Có limx→−1+y=limx→−1+x2+x+1x+1=+∞;limx→−1−y=limx→−1−x2+x+1x+1=−∞

Do đó đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

Có y=x2+x+1x+1=x+1x+1.

Có limx→+∞y−x=limx→+∞x+1x+1−x=limx→+∞1x+1=0;

limx→−∞y−x=limx→−∞x+1x+1−x=limx→−∞1x+1=0.

Do đó đường thẳng y = x là tiệm cận xiên của đồ thị hàm số.

Bài 5. Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức ft=26t+10t+5 (f(t) được tính bằng nghìn người).

Xem y = f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Hãy tìm các đường tiệm cận của đồ thị hàm số.

Hướng dẫn giải

Ta có limt→+∞ft=limt→+∞26t+10t+5=limt→+∞26+10t1+5t=26 .

Do đó y = 26 là tiệm cận ngang của đồ thị hàm số.

Trên nửa khoảng [0; +∞) đồ thị hàm số không có tiệm cận đứng.

Học tốt Đường tiệm cận của đồ thị hàm số

Các bài học để học tốt Đường tiệm cận của đồ thị hàm số Toán lớp 12 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 12 Kết nối tri thức hay khác:

Xem thêm các tài liệu học tốt lớp 12 hay khác:

---