Giải hệ phương trình lớp 9 hay, chi tiết

---

---

Cách giải hệ phương trình lớp 9 với phương pháp giải chi tiết và bài tập đa dạng giúp học sinh
ôn tập, biết cách làm bài tập hệ phương trình.

Giải hệ phương trình Toán lớp 9

A. Phương pháp giải

• Bước 1: Từ một phương trình của hệ phương trình đã cho, ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại để được một phương trình mới (chỉ còn một ẩn).

• Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ phương trình đã cho.

Chú ý:

+ Để có lời giải đơn giản, ta thường chọn các phương trình có hệ số không quá lớn (bằng 1 hoặc -1) và biểu diễn ẩn có hệ số nhỏ hơn qua ẩn còn lại.

+ Thay một phương trình trong hệ bởi phương trình một ẩn vừa tìm ta được hệ phương trình mới tương đương với hệ phương trình đã cho.

B. Bài tập tự luận

Bài 1: Giải các hệ phương trình sau bằng phương pháp thế:

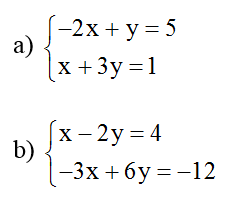
Hướng dẫn giải

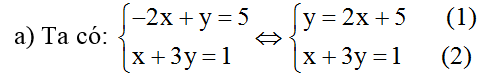
Thế (1) vào (2) ta được: x + 3(2x + 5) = 1

⇔ x + 6x + 15 = 1

⇔ 7x = -14

⇔ x = -2

Thay x = -2 vào (1) ta được y = 2.(-2) + 5 = 1

Vậy hệ phương trình có nghiệm duy nhất (-2;1)

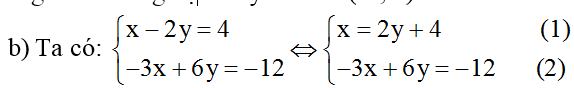
Thế (1) vào (2) ta được: -3(2y + 4) + 6y = -12

⇔ -6y -12 + 6y = -12

⇔ 0y = 0 (luôn đúng)

Vậy hệ phương trình có vô số nghiệm (x;y) thỏa mãn x = 2y +4 và y ∈ R.

Xem thêm:

Bài 2: Cho hàm số y = ax + b. Xác định a, b để đồ thị hàm số đi qua hai điểm M(-1; 2) và N(√3;-7).

Hướng dẫn giải

Do hàm số y = ax + b có đồ thị đi qua M(-1; 2) nên thay x = -1 và y = 2 vào phương trình ta có: 2 = -a + b (1)

Tương tự, hàm số y = ax + b đi qua N(√3;-7) nên ta có: -7 = √3a + b (2)

Bài 3: Trong mặt phẳng Oxy, viết phương trình đường thẳng AB trong các trường hợp:

a) A(-1; 1) và B(2; 4)

b) A(0; -1) và B(1; 0)

Hướng dẫn giải

Gọi phương trình đường thẳng cần tìm là y=ax+b

Vì đường thẳng đi qua A(-1; 1) nên ta có: 1=-a+b (1)

Vì đường thẳng đi qua B(2;4) nên ta có: 4=2a+b (2)

Từ (1) và (2) => a = 3 và b = 4

Vậy phương trình đường thẳng cần tìm là y = 3x + 4.

b, Gọi phương trình đường thẳng cần tìm là y = ax + b

Vì đường thẳng đi qua A(0;-1) nên ta có: -1 = 0.a + b ⇔ b = -1.

Vì đường thẳng đi qua B(1;0) nên ta có: 0 = a + b (1)

Thay b = -1 vào (1) ta được a = 1

Vậy đường thẳng cần tìm là y = x – 1.

Bài 4: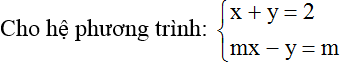

a) Giải hệ phương trình với m = -2.

b) Tìm m để hệ phương trình có nghiệm nguyên.

Hướng dẫn giải

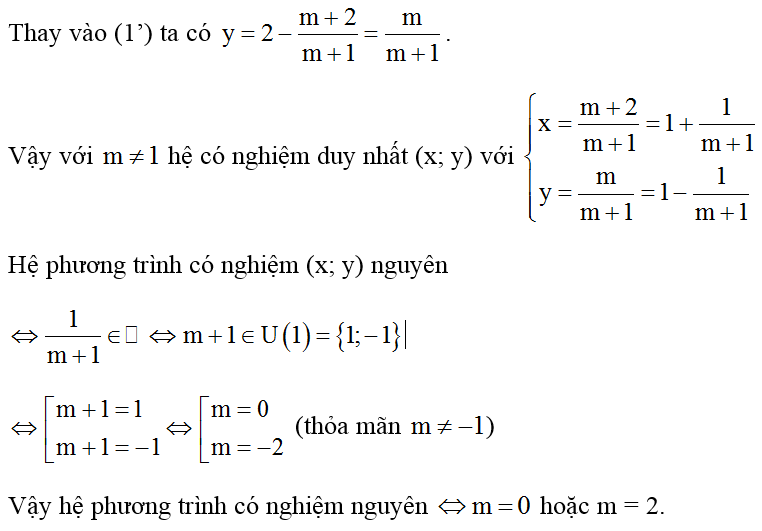
C. Bài tập tự luyện

Bài 1. Giải các phương trình sau:

a) 2x-3y=-5-3x+4y=2;

b) x2-y3=15x-8y=3;

c) 35x-4y=15-2725x+87y=18.

Bài 2. Cho hệ phương trình 2x+13-y+14=4x-2y+252x-34-y-43=-2x+2y-2. Tìm các giá trị của m để nghiệm của hệ phương trình cũng là nghiệm của phương trình 6mx – 5y = 2m – 4.

Bài 3. Giải các hệ phương trình quy về hệ phương trình bậc nhất hai ẩn

a) x+y2=x-y4x3=y5+1;

b) (x-3)(2y+5)=(2x+7)(y-1)(4x+1)(3y-6)=(6x-1)(2y+3);

c) x+y=4x-35x+3y=15-9y14;

d) 7x-7-4x+6=535x-7+3x+6=216;

e) 7x-y+2-5x+y-1=923x-y+2+2x+y-1=4.

Bài 4. Cho đường thẳng d: mx – ny = – 3. Tìm các giá trị của m và n để đường thẳng d’: 4m – 5n = 3 và d đi qua điểm (– 5; 6).

Bài 5. Cho hệ phương trình (m-1)x-my=3m-12x-y=m+5. Hãy xác định giá trị của m để hệ phương trình có nghiệm duy nhất (x, y) sao cho biểu thức: S = x² + y² đạt giá trị nhỏ nhất.

Tham khảo thêm các Chuyên đề Toán lớp 9 khác:

Mục lục các Chuyên đề Toán lớp 9:

---

---

---