Giải toán bằng cách lập hệ phương trình | Chuyên đề Toán 9 – Tuyển tập chuyên đề Toán 9 chọn lọc với đầy đủ phương pháp giải, bài tập tự luận, trắc nghiệm giúp bạn học tốt môn Toán 9.-Giải toán bằng cách lập hệ phương trình – Toán lớp 9
Giải toán bằng cách lập hệ phương trình – Toán lớp 9
Cách giải toán bằng cách lập hệ phương trình lớp 9 với phương pháp giải chi tiết và bài tập đa dạng giúp học sinh
ôn tập, biết cách làm bài tập toán bằng cách lập hệ phương trình.
Giải toán bằng cách lập hệ phương trình
A. Phương pháp giải
Trình tự các bước giải bài toán bằng cách lập hệ phương trình
• Bước 1: Lập hệ phương trình.
+ Biểu diễn hai đại lượng phù hợp bằng ẩn số x và y. Đặt đơn vị và điều kiện của ẩn.
+ Biểu thị các đại lượng chưa biết qua ẩn.
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng và thành lập hệ hai ẩn từ các phương trình vừa tìm.
• Bước 2: Giải hệ phương trình nói trên.
• Bước 3: Kiểm tra nghiệm tìm được thỏa mãn điều kiện của bài toán và nêu kết luận của bài toán.
Xem thêm:
B. Bài tập tự luận
Bài 1: Một mảnh vườn hình chữ nhật có chu vi 34m. Nếu tăng chiều dài thêm 3m và tăng chiều rộng thêm 2m thì diện tích tăng thêm 45m2. Hãy tính chiều dài, chiều rộng của mảnh vườn.
Hướng dẫn giải
Gọi chiều rộng và chiều dài của mảnh vườn là x và y (m, x > 0, y > 0).
Theo đề bài ta có:
Chu vi hình chữ nhật là: 2(x + y) = 34.(1)
Hình chữ nhật mới có chiều dài (y + 3)m, chiều rộng (x +2)m nên có diện tích là (x + 2)(y + 3). Do hình chữ nhật mới có diện tích tăng thêm 45m2 nên ta có phương trình:
(x+2)(y+3)= xy + 45 (2)
Từ (1) và (2) ta có hệ phương trình:
Bài 2: Tìm số có hai chữ số, biết rằng nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là 72 và tổng của số mới và số đã cho là 110.
Hướng dẫn giải
Vậy số cần tìm là 19.
Bài 3: Hai thị xã A và B cách nhau 90km. Một chiếc ôtô khởi hành từ A và một xe máy khởi hành từ B cùng một lúc ngược chiều nhau. Sau khi gặp nhau ôtô chạy thêm 30 phút nữa thì đến B, còn xe máy chạy thêm 2 giờ nữa mới đến A. Tìm vận tốc của mỗi xe.
Hướng dẫn giải
Gọi vận tốc của ôtô và xe máy lần lượt là x và y (km/h, x > 0, y > 0).
Giả sử hai xe gặp nhau tại C. Do ôtô đi hết quãng đường BC trong 30 phút (= 0,5h) và xe máy đi hết quãng đường CA trong 2 giờ nên ta có:
Quãng đường AC dài 2y (km), quãng đường BC dài 0,5x (km).
Thời gian ôtô đi hết quãng đường AC là 2y/x (km/h).
Thời gian xe máy đi trên quãng đường BC là 0,5x/y (km/h).
Do tổng quãng đường AB dài 90km và thời gian hai xe từ lúc xuất phát tới C bằng nhau nên ta có hệ phương trình
Từ (2) suy ra x = 2y (do x > 0, y > 0), thay vào (1) ta có phương trình
3y = 90 ⇔ y = 30 => x = 60 (thỏa mãn x, y > 0).
Vận tốc của ôtô là 60km/h và vận tốc của xe máy là 30km/h.
Bài 4: Một xe máy đi từ A đến B trong một thời gian dự định. Nếu vận tốc tăng thêm 14km/h thì đến B sớm hơn dự định 2 giờ. Nếu giảm vận tốc đi 4km/h thì đến B muộn hơn 1 giờ. Tính vận tốc và thời gian dự định của người đó.
Hướng dẫn giải
Gọi vận tốc dự định là x(km/h) (x > 0)
Thời gian dự định là y (km/h) (y > 0)
Khi đó quãng đường là xy (km/h)
Nếu vận tốc tăng thêm 14km/h thì đến B sớm hơn dự định 2giờ nên ta có phương trình (x+14)(y-2)=xy (1)
Nếu vận tốc giảm đi 4km/h thì đến B muộn hơn 1 giờ nên ta có phương trình (x-4)(y+1)=xy (2)
C. Bài tập tự luyện
Bài 1. Hai năm trước đây, tuổi của anh gấp đôi tuổi của em, còn 8 năm trước đay, tuổi của anh gấp 5 lần tuổi em. Hỏi hiện nay anh và em bao nhiêu tuổi.
Bài 2. Có hai loại quạng chưa 75% sắt và 50% sắt. Tính khối lượng của mỗi loại quặng đem trộn để được 25 tấn quặng chứa 66% sắt.
Bài 3. Một hình chữ nhật có chu vi 90m. Nếu tăng chiều rộng lên gấp đôi và giảm chiều dài đi 15m thì ta được hình chữ nhật mới có diện tích bằng diện tích hình chữ nhật ban đầu. Tính các cạnh của hình chữ nhật đã cho.
Bài 4. Một người dự định đi xe máy từ A đến B cách nhau 96 km trong thời gian nhất định. Sau khi đi được một nửa quãng đường, người đó dừng lại 18 phút. Do đó để đến B đúng hẹn, người đó đã tăng vận tốc thêm 2km/h trên quãng đường còn lại. Tính vận tốc ban đầu và thời gian xe lăn bánh trên đường.
Bài 5. Bạn Tuấn vào cửa hàng bách hóa mua một đoi giày và một bộ quần áo thể thao, giá tiền tổng cộng là 148.000 đồng. Một tuần sau trở lại giá mỗi đôi giày giảm 20%, giá mỗi bộ quần áo thể thao đã giảm 40%. Bạn Tuấn đưa cho cô bán hàng 11.000 đồng, cô bán hàng trả lại bạn Tuấn 8.900 đồng. Hỏi giá tiền một đôi giày, giá tiền một bộ quần áo thể thao khi chưa giảm giá là bao nhiêu?
Tham khảo thêm các Chuyên đề Toán lớp 9 khác:
Mục lục các Chuyên đề Toán lớp 9:

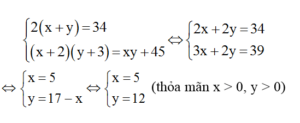

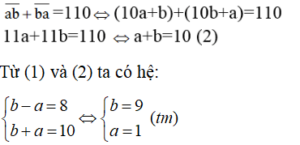

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: [email protected]