Hãy tìm bậc của mỗi đa thức sau: M = x^2 – 2xy + 5x^2 – 1; N = x^2y^2 – y^2 + 5x^2 – 3x^2y + 5

---

---

Bài 8: Cộng, trừ đa thức một biến

Luyện tập trang 46 sgk Toán 7 Tập 2

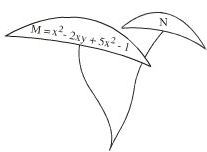
Bài 49 trang 46 sgk Toán lớp 7 Tập 2: Hãy tìm bậc của mỗi đa thức sau:

    M = x² – 2xy + 5x² – 1

    N = x²y² – y² + 5x² – 3x²y + 5

Lời giải:

a) Rút gọn đa thức M ta có :

M = x² – 2xy + 5x² – 1 = (x²+ 5x²) – 2xy – 1 = 6x² – 2xy – 1

Sau khi rút gọn, M có các hạng tử là:

6x² có bậc 2

– 2xy có bậc 2

– 1 có bậc 0

Bậc của đa thức là bậc của hạng tử có bậc cao nhất

⇒ Đa thức M = x² – 2xy + 5x² – 1 có bậc 2.

b) N = x²y² – y² + 5x² – 3x²y + 5 có các hạng tử là

x²y² có bậc 4 (vì biến x có bậc 2, biến y có bậc 2, tổng là 2 + 2 = 4)

– y² có bậc 2

5x² có bậc 2

– 3x²y có bậc 3 (vì biến x có bậc 2, biến y có bậc 1, tổng là 2 + 1 = 3)

5 có bậc 0

Bậc của đa thức là bậc của hạng tử có bậc cao nhất.

⇒ Đa thức N = x²y² – y² + 5x² – 3x²y + 5 có bậc 4

Kiến thức áp dụng

Xem thêm các bài giải bài tập Toán lớp 7 Bài 8 khác:

Lời giải bài tập lớp 7 sách mới:

---

---

---