Hệ trục toạ độ trong không gian (Lý thuyết Toán lớp 12) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 12 Bài 7: Hệ trục toạ độ trong không gian sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Hệ trục toạ độ trong không gian (Lý thuyết Toán lớp 12) | Kết nối tri thức

Lý thuyết Hệ trục toạ độ trong không gian

1. Hệ trục tọa độ trong không gian

Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi i→,j→,k→ lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz.

• Hệ ba trục như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz, hay đơn giản là hệ tọa độ Oxyz.

• Điểm O được gọi là gốc tọa độ.

• Các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau được gọi là các mặt phẳng tọa độ.

Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.

Ví dụ 1. Một góc nhà với hệ tọa độ Oxyz được chọn như hình vẽ. Hãy cho biết mặt sàn của góc nhà nằm trong mặt phẳng tọa độ nào?

Hướng dẫn giải

Mặt sàn của góc nhà nằm trong mặt phẳng (Oxy).

2. Tọa độ của điểm, tọa độ của vectơ trong không gian

• Tọa độ của điểm trong không gian

Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho O⁢M→=x⁢i→+y⁢j→+z⁢k→ được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết M = (x; y; z) hoặc M(x; y; z), trong đó x là hoành độ, y là tung độ và z là cao độ của M.

Ví dụ 2. Cho hệ tọa độ Oxyz sau. Hãy xác định tọa độ điểm M.

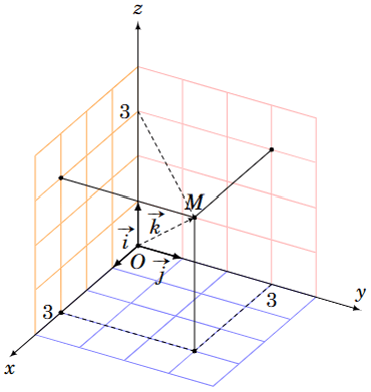
Hướng dẫn giải

Ta có O⁢M→=3⁢i→+3⁢j→+3⁢k→.

Do đó M(3; 3; 3).

Nhận xét: Nếu điểm M có tọa độ (x; y; z) đối với hệ tọa độ Oxyz thì:

– Hình chiếu vuông góc của M trên các trục Ox, Oy và Oz có tọa độ lần lượt là (x; 0; 0), (0; y; 0) và (0; 0; z).

– Hình chiếu vuông góc của M trên các mặt phẳng (Oxy), (Oyz) và (Ozx) có tọa độ lần lượt là (x; y; 0), (0; y; z), (x; 0; z).

Ví dụ 3. Trong không gian Oxyz, cho các điểm A(1; 0; 2), B(2; 3; 0), C(−1; 0; 0), D(0; 0; 1), E(0; −1; −1), F(0; 2; 0). Trong các điểm đã cho, điểm nào thuộc

a) mặt phẳng (Oxy);

b) mặt phẳng (Oyz);

c) mặt phẳng (Oxz);

d) trục Ox;

e) trục Oy;

f) trục Oz?

Hướng dẫn giải

a) Điểm thuộc mặt phẳng (Oxy) là B(2; 3; 0).

b) Điểm thuộc mặt phẳng (Oyz) là E(0; −1; −1).

c) Điểm thuộc mặt phẳng (Oxz) là A(1; 0; 2).

d) Điểm thuộc trục Ox là C(−1; 0; 0).

e) Điểm thuộc trục Oy là F(0; 2; 0).

f) Điểm thuộc trục Oz là D(0; 0; 1).

• Tọa độ của vectơ trong không gian

Trong không gian Oxyz, cho vectơ a→ tùy ý. Bộ ba số (x; y; z) duy nhất sao cho a→=x⁢i→+y⁢j→+z⁢k→ được gọi là tọa độ của vectơa→ đối với hệ tọa độ Oxyz. Khi đó, ta viết a→=(x;y;z) hoặc a→⁢(x;y;z).

Nhận xét:

– Tọa độ của vectơ cũng là tọa độ của điểm M sao cho O⁢M→=a→

– Trong không gian, cho hai vectơ a→=(x;y;z) và b→=(x’;y’;z’). Khi đó, a→=b→ nếu và chỉ nếu x=x’y=y’z=z’.

Ví dụ 3. Trong không gian Oxyz, cho v→=i→+2⁢k→  và u→=i→+2⁢j→-3⁢k→. Xác định tọa độ của các vectơ u→ và v→.

Hướng dẫn giải

Có u→=i→+2⁢j→-3⁢k→⇒u→=(1;2;-3).

v→=i→+2⁢k→⇒v→=(1;0;2).

• Tọa độ của vectơ theo tọa độ hai đầu mút

Trong không gian Oxyz, cho hai điểm M(x_M; y_M; z_M) và N(x_N; y_N; z_N). Khi đó: M⁢N→=(xN-xM;yN-yM;zN-zM).

Ví dụ 4. Trong không gian Oxyz cho ba điểm A(1; 2; −3), B(−2; 4; 5), C(7; −3; −5).

a) Tìm tọa độ A⁢B→,B⁢C→.

b) Tìm điểm D(x; y; z) sao cho tứ giác ABCD là hình bình hành.

Hướng dẫn giải

a) A⁢B→=(-2-1;4-2;5+3)=(-3;2;8) và B⁢C→=(7+2;-3-4;-5-5)=(9;-7;-10).

b) Để ABCD là hình bình hành thì A⁢D→=B⁢C→.⇔x – 1 = 9y – 2 =  – 7z + 3 =  – 10

⇔x = 10y =  – 5z =  – 13

Vậy D(10; −5; −13).

Bài tập Hệ trục toạ độ trong không gian

Bài 1. Trong không gian Oxyz, cho điểm M thỏa mãn hệ thức O⁢M→=2⁢i→+j→. Tọa độ của điểm M là

A. M(0; 2; 1).             

B. M(2; 0; 1).                                    

C. M(2; 1; 0).                                    

D. M(0; 1; 2).

Hướng dẫn giải

Đáp án đúng là: C

Ta có O⁢M→=2⁢i→+j→ ⇒M⁢(2;1;0) .

Bài 2. Trong không gian với hệ tọa độ Oxyz, điểm nào sau đây thuộc mặt phẳng (Oxy)

A. N(1; 0; 2).              

B. P(0; 1; 2).                                    

C. Q(0; 0; 2).                                    

D. M(1; 2; 0).

Hướng dẫn giải

Đáp án đúng là: D

Điểm M(1; 2; 0) thuộc mặt phẳng (Oxy).

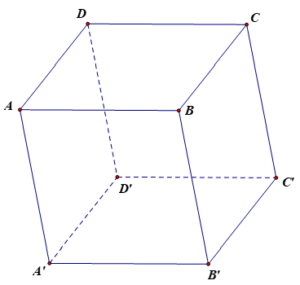
Bài 3. Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’, biết rằng A(−3; 0; 0), B(0; 2; 0), D(0; 0; 1), A'(1; 2; 3). Tìm tọa độ điểm C’.

Hướng dẫn giải

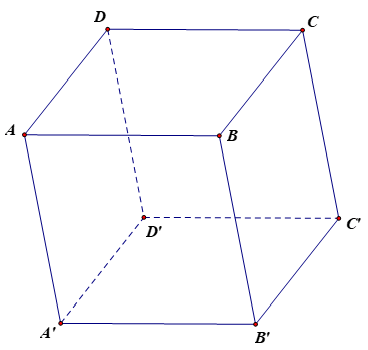
Ta có A⁢D→=(3;0;1). Gọi C(x; y; z)

Vì ABCD là hình bình hành nên A⁢D→=B⁢C→⇔x=3y-2=0z=1⇔x=3y=2z=1.

Suy ra C(3; 2; 1).

Có A⁢A’→=(4;2;3). Gọi C'(a; b; c).

Vì AA’C’C là hình bình hành nên A⁢A’→=C⁢C’→⇔a-3=4b-2=2c-1=3⇔a=7b=4c=4.

Vậy C'(7; 4; 4).

Bài 4. Trong không gian Oxyz, cho ba điểm M(0; 1; 2), N(7; 3; 2), P(−5; −3; 2).

a) Tìm tọa độ vectơ M⁢N→.

b) Tìm tọa độ điểm Q thỏa mãn M⁢N→=Q⁢P→.

Hướng dẫn giải

a) Có M⁢N→=(7-0;3-1;2-2)=(7;2;0).

b) Gọi Q(x; y; z).

Vì M⁢N→=Q⁢P→ nên -5-x=7-3-y=22-z=0⇔x=-12y=-5z=2 . Vậy Q(−12; −5; 2).

Bài 5. Hình a mô tả một sân cầu lông với kích thước theo tiêu chuẩn quốc tế. Ta chọn hệ trục Oxyz cho sân đó như hình b (đơn vị trên mỗi trục là mét). Giả sử AB là một trụ cầu lông để căng lưới. Hãy xác định tọa độ của vectơ A⁢B→.

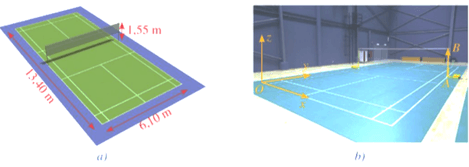
Hướng dẫn giải

Gọi tọa độ điểm A là (x_A; y_A; z_A). Vì chiều rộng của sân là 6,1 m nên x_A = 6,1.

Do nửa chiều dài của sân là 6,7 m nên y_A = 6,7.

Điểm A thuộc mặt phẳng (Oxy) nên z_A = 0.

Vậy A(6,1; 6,7; 0).

Độ dài đoạn thẳng AB là 1,55 m nên điểm B có tọa độ là (6,1; 6,7; 1,55).

Vậy ta có A⁢B→=(6,1-6,1;6,7-6,7;1,55-0)=(0;0;1,55).

Học tốt Hệ trục toạ độ trong không gian

Các bài học để học tốt Hệ trục toạ độ trong không gian Toán lớp 12 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 12 Kết nối tri thức hay khác:

Xem thêm các tài liệu học tốt lớp 12 hay khác:

---