Hình thang cân (Lý thuyết Toán lớp 8) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 8 Bài 11: Hình thang cân sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Hình thang cân (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Hình thang cân

1. Hình thang. Hình thang cân

+ Hình thang là tứ giác có hai cạnh đối song song.

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Xét các hình dưới đây:

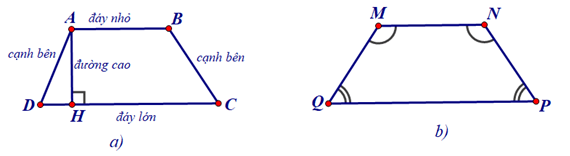
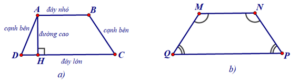
+ Hình a là hình thang ABCD (AB // CD). Hai cạnh song song gọi là hai đáy, hai cạnh còn lại gọi là hai cạnh bên, đường vuông góc AH kẻ từ A đến CD gọi là một đường cao của hình thang ABCD.

+ Hình b là hình thang cân MNPQ  (MN // PQ)

Hai góc M, N kề đáy nhỏ MN, M^=N^

Hai góc C, D kề đáy lớn CD, C^=D^ .

Chú ý: Trong hình thang, hai góc kề một đáy bằng nhau thì hai góc kề đáy kia cũng bằng nhau.

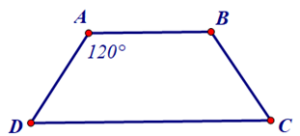
Ví dụ 1: Tính các góc của hình thang cân ABCD (AB // CD) biết A^=120°.

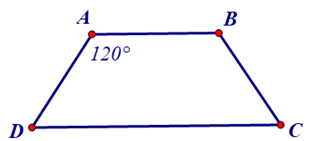
Vì ABCD (AB // CD) là hình thang cân nên B^=A^=120°.

Do A^+D^=180°  (hai góc kề bù) nên D^=180°−A^=180°−120°=60° .

⇒C^=D^=60°.

2. Tính chất của hình thang cân

+ Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.

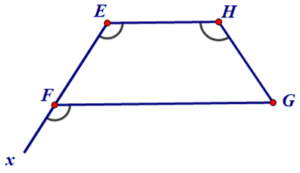
Ví dụ 2: Cho tứ giác EFGH như hình dưới, biết  E^=H^=xFG^.

Chứng minh EF = HG.

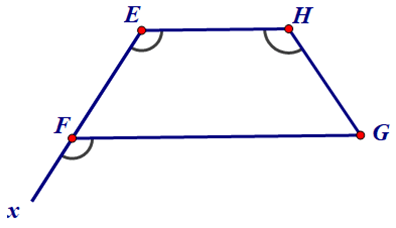
Hướng dẫn giải

Ta có: E^=xFG^  mà hai góc này ở vị trí đồng vị nên EH // FG suy ra EFGH là hình thang.

Hình thang EFGH có E^=H^  (hai góc kề đáy EH bằng nhau) nên EFGH là hình thang cân

EF = GH (hai cạnh bên bằng nhau).

+ Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.

Ví dụ 3: (Chứng minh Định Lí 2) Cho hình thang cân MNEF (MN // EF), chứng minh ME = NF.

Hướng dẫn giải

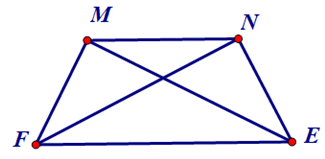
Vì MNEF (MN // EF) là hình thang cân nên FMN^=MNE^  và MF = NE.

Xét ΔMNF và ΔNME  có:

MF = NE

FMN^=MNE^

MN chung

Do đó ΔMNF=ΔNME  (cạnh – góc – cạnh)

Suy ra ME = NF (cạnh tương ứng bằng nhau).

3. Dấu hiệu nhận biết

+ Định lí 3 (Dấu hiệu nhận biết hình thang cân): Nếu một hình thang có hai đường chéo bằng nhau thì đó là hình thang cân.

Chú ý: Định lí 3 là định lí đảo của định lí 2. Giả thiết của định lí này là kết luận của định lí kia.

Bài tập Hình thang cân

Bài 1. Hình thang ABCD (AB // CD) trong hình bên dưới có phải hình thang cân không? Vì sao?

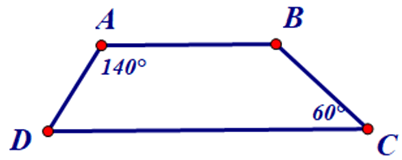
Hướng dẫn giải

Giả sử ABCD (AB // CD) là hình thang cân.

Khi đó, ta có: A^=B^=140°, C^=D^=60°.

Tổng 4 góc trong hình thang ABCD là A^+B^+C^+D^=400°>360° .

Suy ra ABCD không phải là hình thang cân.

Bài 2. Cho hình thang MNPQ (MN // PQ) có NMP^=MNQ^,  E là giao điểm của MP và NQ. Chứng minh hình thang MNPQ là hình thang cân.

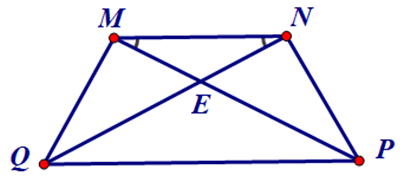
Hướng dẫn giải

Vì MN // QP nên NMP^=MPQ^  và NQP^=MNQ^(các cặp góc so le trong)

Mà NMP^=MNQ^⇒NMP^=MPQ^=NQP^=MNQ^.

ΔMNE có NMP^=MNQ^ nên ΔMNEcân tại E

Suy ra ME = NE (1)

ΔQEP có MPQ^=NQP^  nên ΔQEP  cân tại E

Suy ra EQ = EP (2)

Từ (1) và (2) ta có: ME + EP = NE +  EQ hay MP = NQ

Suy ra MNPQ là hình thang cân (dấu hiệu nhận biết).

Bài 3. Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

Hướng dẫn giải

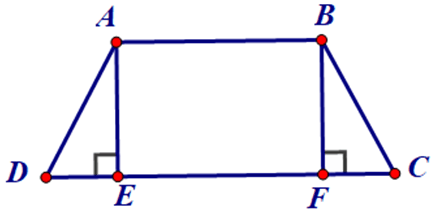
Vì ABCD (AB // CD) là hình thang cân nên D^=C^ và AD = BC.

Xét ΔAED  và ΔBFC  có: 

AED^=BFC^=90° (AE⊥DC, BF⊥DC)

D^=C^(chứng minh trên)

AD = BC (chứng minh trên)

Do đó ΔAED=ΔBFC  (cạnh huyền – góc nhọn)

Suy ra DE = CF (cạnh tương ứng bằng nhau).

Học tốt Hình thang cân

Các bài học để học tốt Hình thang cân Toán lớp 8 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay khác:

Xem thêm các tài liệu học tốt lớp 8 hay khác:

---