Khoảng cách giữa hai đường thẳng chéo nhau lớp 11 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Khoảng cách giữa hai đường thẳng chéo nhau lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện
đa dạng giúp học sinh ôn tập, biết cách làm bài tập Khoảng cách giữa hai đường thẳng chéo nhau.

Khoảng cách giữa hai đường thẳng chéo nhau lớp 11 (cách giải + bài tập)

1. Phương pháp giải

Để tính khoảng cách giữa hai đường thẳng chéo nhau ta dựng đoạn vuông góc chung MN của a và b. Khi đó d(a, b) = MN. Sau đây là một số cách dựng đoạn vuông góc chung thường dùng:

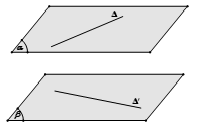
Phương pháp 1: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó d(∆, ∆’) = d(∆’, (α)).

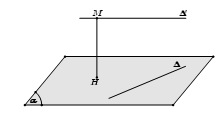
Phương pháp 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.

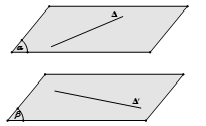
 Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.

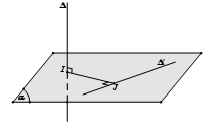
– Trường hợp 1:  ∆ và ∆’ vừa chéo nhau vừa vuông góc với nhau.

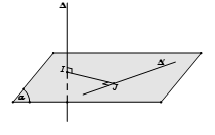
Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I.

Bước 2: Trong mặt phẳng (α) kẻ IJ ⊥ ∆’.

Khi đó IJ là đoạn vuông góc chung và d(∆, ∆’) = IJ.

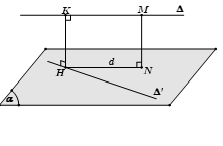
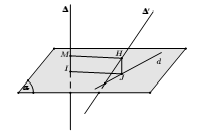
– Trường hợp 2:  ∆ và ∆’ vừa chéo nhau và không vuông góc với nhau.

Bước 1: Chọn mặt phẳng (α) chứa ∆’ và song song với ∆.

Bước 2: Dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm M∈ ∆ dựng đoạn MN ⊥ (α), lúc đó d là đường thẳng đi qua N và song song với ∆.

Bước 3: Gọi H = d ∩ ∆’, dựng HK // MN.

Khi đó HK là đoạn vuông góc chung và d(∆, ∆’) = HK = MN.

Hoặc

Bước 1: Chọn mặt phẳng (α)⊥ ∆ tại I.

Bước 2: Tìm hình chiếu d của ∆’ xuống mặt phẳng (α).

Bước 3: Trong mặt phẳng (α), dựng IJ ⊥ d, từ J dựng đường thẳng song song với ∆ cắt ∆’ tại H, từ H dựng HM // IJ.

Khi đó HM là đoạn vuông góc chung và d(∆, ∆’) = HM = IJ.

2. Ví dụ minh họa

Ví dụ 1. Cho hình chóp S.ABCD có đáy hình vuông ABCD tâm O cạnh a2 , cạnh SA=a2  và vuông góc mặt đáy.

a) Tính khoảng cách giữa BC và SD.

b) Tính khoảng cách giữa SC và AD.

Hướng dẫn giải:

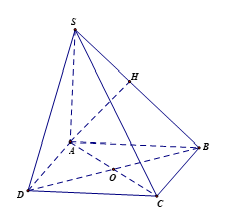
a) Vì SA ⊥ (ABCD) ⇒ SA ⊥ CD.

Do ABCD là hình vuông nên CD ⊥ AD.

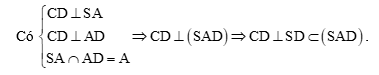
Ta có: CD ⊥ SD tại D, CD ⊥ BC tại C.

⇒ CD là đoạn vuông góc chung của SD và BC.

⇒ d(SD, BC) = CD = 2a.

b) Vì AD // BC mà BC⊂ (SBC) ⇒ AD // (SBC).

Do đó d(AD, SC) = d(AD, (SBC)) = d(A, (SBC)).

Kẻ AH ⊥ SB tại H.

Có SA⊥ (ABCD) ⇒ SA ⊥BC mà BC ⊥ AB ⇒ BC ⊥(SAB) ⇒ BC ⊥AH.

Lại có AH ⊥ SB nên AH ⊥ (SBC).

Do đó d(A, (SBC)) = AH.

Xét ∆SAB vuông tại A, có 1AH2=1SA2+1AB2=12a2+12a2=1a2⇒AH=a.

Vậy d(SC, AD) = a.

Ví dụ 2. Cho lăng trụ đứng ABCD.A’B’C’D’ có tất cả các cạnh bằng a, góc DAB^=120° .

a) Tính khoảng cách giữa BD và CC’.

b) Tính khoảng cách giữa AC và BD’.

Hướng dẫn giải:

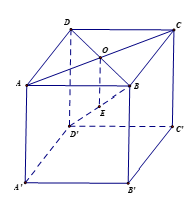
a) Gọi O là tâm của hình thoi ABCD.

Vì ABCD là hình thoi nên O là trung điểm của AC, BD và AC ⊥ BD.

Xét DABD có BD² = AB² + AD² – 2AB.AD.cos120° = 3a²

⇒ BD=a3⇒BO=a32

Xét DAOB vuông tại O, có AO=AB2−BO2=a2−3a24=a2  ⇒ AC = a.

Vì CC’ ⊥ (ABCD) ⇒ CC’ ⊥ CO mà CO⊥ BD nên CO là đoạn vuông góc chung của BD và CC’.

Do đó d(BD, CC’) = CO = AO = a2 .

b) Trong (BDD’B’) kẻ OE ⊥ BD’ tại E (1).

Vì AC ⊥ BD và AC ⊥ DD’ (DD’ ⊥ (ABCD)) ⇒ AC ⊥ (BDD’B’)⇒ AC ⊥OE (2).

Từ (1) và (2), suy ra OE là đoạn vuông góc chung của AC và BD’.

Do đó d(AC, BD’) = OE.

Mà OE = d(O, BD’) = 12dD,BD’.

Gọi h là khoảng cách từ D đến BD’.

Xét DD’DB vuông tại D, có 1h2=1DD’2+1DB2=1a2+13a2=43a2⇒h=a32 .

Vậy d(AC, BD’) = a34 .

3. Bài tập tự luyện

Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi K, H theo thứ tự là hình chiếu vuông góc của A và O lên SD. Chọn khẳng định đúng trong các khẳng định sau?

A.Đoạn vuông góc chung của AC và SD là AK;

B.Đoạn vuông góc chung của AC và SD là CD;

C.Đoạn vuông góc chung của AC và SD là OH;

D.Các khẳng định trên đều sai.

Bài 2. Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD.

A. a32 ;

B. a23;

C. a22;

D. a33.

Bài 3. Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật với AC=a5 và BC=a2 . Tính khoảng cách giữa SD và BC.

A. 3a4 ;

B. 2a3;

C. a32;

D. a3.

Bài 4. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa BB’ và AC bằng:

A. a2 ;

B. a3;

C. a22;

D. a33.

Bài 5. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Khoảng cách giữa AA’ và BD’ bằng:

A. 33 ;

B. 22 ;

C. 225;

D. 357.

Bài 6. Cho khối lập phương ABCD.A’B’C’D’. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A’C’ là:

A. AA’;

B. BD;

C. DA’;

D. DD’.

Bài 7. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau?

A. a;

B. a2 ;

C. a3 ;

D. 2a.

Bài 8. Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc với nhau, OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu?

A. a;

B. a5 ;

C. a32 ;

D. a2 .

Bài 9. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với mặt đáy và SA = a. Tính khoảng cách giữa SB và CD.

A. a24 ;

B. a2 ;

C. a33 ;

D. a22 .

Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h.  Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BD.

A. ah3a2+h2 ;

B. aha2+h2 ;

C. ah2a2+h2 ;

D. aha2+2h2 .

Xem thêm các dạng bài tập Toán 11 hay, chi tiết khác:

---