Lý thuyết Các hệ thức lượng trong tam giác và giải tam giác lớp 10 (hay, chi tiết)

---

---

Bài viết Lý thuyết Các hệ thức lượng trong tam giác và giải tam giác lớp 10 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Các hệ thức lượng trong tam giác và giải tam giác.

Lý thuyết Các hệ thức lượng trong tam giác và giải tam giác

Bài giảng: Bài 3: Các hệ thức lượng trong tam giác và giải tam giác – Thầy Lê Thành Đạt (Giáo viên VietJack)

A. Phương pháp giải

1. Định lí côsin

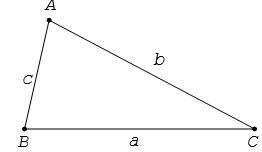
Cho tam giác ABC có BC = a, AC = b và AB = c

Ta có

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

Hệ quả

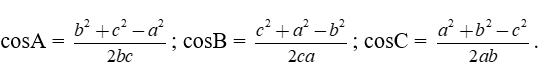
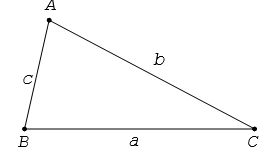
2. Định lí sin

Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.

Ta có

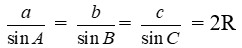
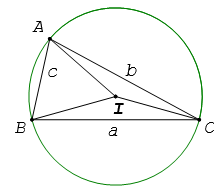
3. Độ dài đường trung tuyến

Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.

Ta có

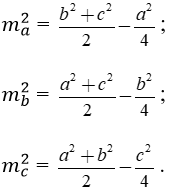
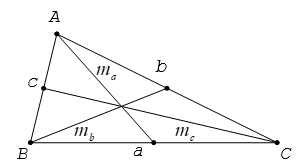
4. Công thức tính diện tích tam giác

Cho tam giác ABC có

+) ha, hb, hc là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB;

+) R là bán kính đường tròn ngoại tiếp tam giác;

+) r là bán kính đường tròn nội tiếp tam giác;

+) p = 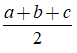là nửa chu vi tam giác;

+) S là diện tích tam giác.

Khi đó ta có:

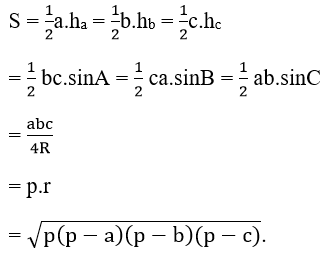
B. Bài tập tự luyện

Ví dụ minh họa hoặc bài tập có giải

Ví dụ 1. Cho tam giác ABC có AB = 1cm , AC = 2cm. Tính BC.

Hướng dẫn giải

Áp dụng định lí Cosin ta có:

BC² = AB² + AC² – 2AB.AC.cosA

= 1² + 2² – 2.1.2.cos120°

= 1+ 4 – 4.−12 = 7

Suy ra BC = 7 cm.

Ví dụ 2. Cho tam giác ABC có AB = 23, AC = 24, B = 60º. Tính sin của góc C.

Hướng dẫn giải

Áp dụng định lí sin ta có: ABsinC=ACsinB.

sinC=ABsinBAC=23.sin60°24=23348.

Ví dụ 3. Cho hình bình hành ABCD, chứng minh rằng BD² + AC² = 2.(AB² + AD²).

Hướng dẫn giải

Ta có O là tâm hình bình hành ABCD, O là trung điểm của AC

BO là trung tuyến của tam giác ABC ứng với cạnh AC nên

BO2=BC2+BA22−AC24

Hay 4BO² = 2(BC² + BA²) – AC² (1)

Mà O là trung điểm của BD nên BD = 2BO => BD² = 4BO²

(1) => BD² = 2(CB² + AB²) – AC² 

=> BD² + AC² = 2(CB² + AB²) 

=> BD² + AC² = 2(AB² + AD²) (do AD = CB ) (điều cần phải chứng minh)

Ví dụ 4. Cho tam giác ABC. Chứng minh góc A nhọn khi và chỉ khi BC² < AB² + AC².

Hướng dẫn giải

Áp dụng định lí Cos, ta có:

cosA=AB2+AC2−BC22AB.AC

Mà AB.AC luôn lớn hơn 0 nên cos A cùng dấu với biểu thức (AB² + AC² – BC²)

Góc A là góc nhọn

=> 0º < A < 90º

=> cos A > 0

=> AB² + AC² – BC² > 0

=> BC² < AB² + AC²

Ví dụ 5. Một ô tô đi từ A đến C nhưng giữa A và C là một ngọn núi cao nên ô tô phải chạy thành hai đoạn đường từ A đến B và từ B đến C, các đoạn đường này tạo thành tam giác ABC có AB =15 km, BC = 10 km và góc B = 105º. Giả sử người ta khoan hầm qua một núi và tạo ra một con đường thẳng từ A đến C, tính độ dài đoạn đường này.

Hướng dẫn giải

Áp dụng định lí Cosin ta có:

AC² = AB² + BC² = 2AB.BC.cos B

=> AC² = 15² + 10² – 2 . 15 . 10 . cos 105º ≈ 402,65

=> AC = 402,65 ≈ 20,07 (km)

Bài tập bổ sung

Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9 cm. Tính độ dài BC và AH.

Hướng dẫn giải

Ta đặt HC = x (x > 0).

Áp dụng hệ thức lượng vào tam giác ABC, ta có

AC² = BC.HC, ta được:

20² = (9 + x)x

x² + 9x – 400 = 0

(x + 25)(x – 16) = 0

x = –25 (loại) hoặc x = 16 (TM)

Vậy độ dài của cạnh huyền BC là:

BC = BH + HC = 9 + 16 = 25 (cm)

Ta có: AH² = HB.HC = 9.25 = 225

Do đó, chiều dài đường cao AH là: AH = 15 cm.

Bài 2. Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của các góc nhọn α, β: cos2α.cos2β + cos2α.sin2β + sin2α

Hướng dẫn giải

Ta có

cos2α.cos2β + cos2α.sin2β + sin2α

= cos2α(cos2β + sin2β) + sin2α

= cos2α.1 + sin2α = 1.

Bài 3. Cho tam giác ABC vuông tại A, AB : AC = 7 : 24, BC = 625 cm. Tính độ dài hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Hướng dẫn giải

Vẽ AH ⊥ BC, thì ta có: AB² = BH.BC; AC² = CH.BC.

Khi đó, ta có AB2AC2=BHCH hay 72242=BHCH.

Do đó BHCH=49576.

Nên ta có BH49=CH576=BH+CH49+576=BC625=625625=1.

Vậy BH = 49.1 = 49; CH = 576.1 = 576.

Bài 4. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB = 3 cm, AC = 4 cm. Tính độ dài các đoạn thẳng BH, CH, AH và BC.

Hướng dẫn giải

Ta thấy ngay có thể tính cạnh huyền của tam giác ABC:

BC² = AB² + AC² = 3² + 4² = 25 suy ra BC = 5 cm.

Vậy ta có độ dài hai cạnh góc vuông và cạnh huyền, giờ có thể tính BH và CH dựa vào công thức liên quan đến hình chiếu, cạnh huyền và cạnh góc vuông.

Ta có: AB² = BH.BC suy ra BH = AB2BC=325=95 (cm)

Tương tự, AC² = HC.BC suy ra HC = AC2BC = 165 (cm)

Tính AH dựa vào hệ thức h² = b’.c’ tức là

AH² = BH.CH = 14425 suy ra AH = 125 cm

Bài 5. Cho tam giác ABC vuông tại A, AH vuông góc BC (H ∈ BC). Biết AB : AC = 3 : 4 và BC = 15 cm. Tính độ dài các đoạn thẳng BH và HC.

Hướng dẫn giải

AB : AC = 3 : 4

Ta gọi AB = 3k, AC = 4k.

Áp dụng định lí Pythagore vào tam giác vuông ABC:

AB² + AC² = BC² suy ra 9k² + 16k² = 15² suy ra k² = 15225 = 9, vậy k = 3.

Từ đó suy ra AB = 9 cm, AC = 12 cm.

Ta áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:

• AB² = BH.BC suy ra BH = AB2BC = 275 (cm)

• AC² = HC.BC suy ra HC = AC2BC = 485 (cm).

Bài 6. Cho DABC có a = 12, b = 15, c = 13. Tính số đo các góc của DABC.

Bài 7. Cho DABC có AB = 6, AC = 8, A^=120°. Tính cạnh BC và bán kính R.

Bài 8. Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của các góc nhọn α, β:

2(sinα – cosα )² – (sinα + cosα )² + 6sinα.cosα

Bài 9. Cho DABC có a = 8, b = 10, c = 13. Tính diện tích DABC.

Bài 10. Cho DABC có AC = 7, AB = 5 và cos A = 35. Tính BC, S, h_a, R.

Xem thêm các bài giảng lý thuyết và các dạng bài tập Toán lớp 10 chọn lọc, có đáp án khác:

Lời giải bài tập lớp 10 sách mới:

---

---

---