Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba đầy đủ nhất

---

---

Bài viết Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba lớp 9 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Chương 1: Căn bậc hai, Căn bậc ba.

Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba đầy đủ nhất

1. Căn bậc hai số học

    – Căn bậc hai số học của số thực a không âm là số không âm x mà x² = a

    – Với a ≥ 0

x = √a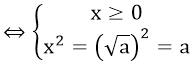

Phép toán tìm căn bậc hai số học của một số gọi là phép khai phương

Với hai số a, b không âm, thì ta có: a < b ⇔ √a < √b

2. Căn thức bậc hai

    – Cho A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.

    – √A xác định (hay có nghĩa) khi A ≥ 0

    – Hằng đẳng thức √(A²) = |A|

3. Chú ý

      +) Với a ≥ 0 thì:

√x = a ⇒ x = a²

x² = a ⇒ x = ± √a

      +) √A = √B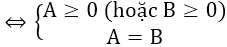

      +) √A + √B = 0 ⇔ A = B = 0

1.

Với A ≥ 0, B ≥ 0 thì √(A.B) = √A . √B và ngược lại √A . √B = √(A.B)

Đặc biệt, khi A ≥ 0, ta có: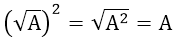

2.

Với A ≥ 0, B > 0 thì: 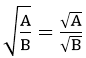và ngược lại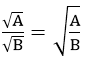

3. Bổ sung

      +) Với A₁, A₂, …, A_n ≥ 0 thì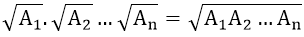

      +) Với a ≥ 0; b ≥ 0 thì 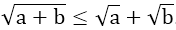. Dấu bằng xảy ra khi a = 0 hoặc b = 0

      +) Với a ≥ b ≥ 0 thì 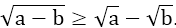. Dấu bằng xảy ra khi a = 0 hoặc b = 0

4. Các bất đẳng thức thường dùng

      +) Với a ≥ b ≥ 0 thì a + b ≥ 2√(ab)

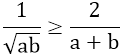      +) với a > 0; b > 0

1. Đưa thừa số ra ngoài dấu căn

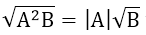với B ≥ 0

2. Đưa thừa số vào trong dấu căn

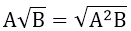với A ≥ 0; B ≥ 0

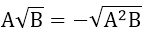với A < 0; B ≥ 0

3. Khử mẫu ở biểu thức chứa căn

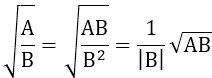với AB ≥ 0; B ≠ 0

4. Trục căn thức ở mẫu

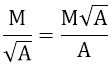(A > 0)

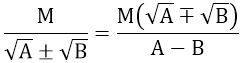(A ≥ 0 ; B ≥ 0; A ≠ B)

5. Rút gọn biểu thức có chứa căn bậc hai

Bước 1: Dùng các phép biến đổi đơn giản để đưa các căn thức bậc hai phức tạp thành căn thức bậc hai đơn giản.

Bước 2: Thực hiện các phép tính theo thứ tự đã biết.

1. Định nghĩa: Căn bậc ba của một số a, kí hiệu là ³√a là số x sao cho x³ = a.

      +) Cho a ∈ R; ³√a = x ⇔ x³ = (³√a)³ = a

      +) Mỗi số thực a đều có duy nhất một căn bậc ba

      +) Nếu a > 0 thì ³√a > 0

      +) Nếu a = 0 thì ³√a = 0

      +) Nếu a < 0 thì ³√a < 0

2. Tính chất

      +) a < b ⇔ ³√a < ³√b

      +)

      +)

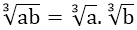
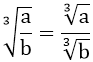
3. Các phép biến đổi căn bậc ba

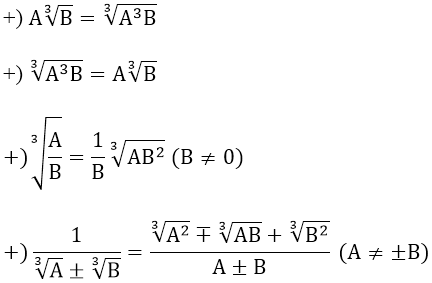
    – Hai biểu thức √a + √b và √a – √b gọi là hai biểu thức liên hợp.

    – Hai biểu thức 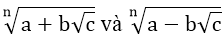trong đó a, b, c là các biểu thức, gọi là hai biểu thức liên hợp bậc n.

Khi gặp các bài tập tính toán, rút gọn,… có dạng tổng hay hiệu của hai biểu thức liên hợp thì có thể dùng phép lũy thừa để khử bớt dấu căn.

Chuyên đề Toán 9: đầy đủ Lý thuyết và các dạng bài tập có đáp án khác:

---

---

---