Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông đầy đủ nhất

Bài viết Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông lớp 9 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Chương 1: Hệ thức lượng trong tam giác vuông.

Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông đầy đủ nhất

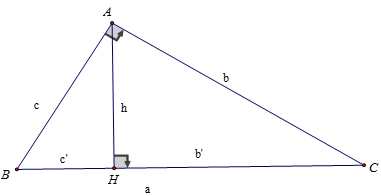
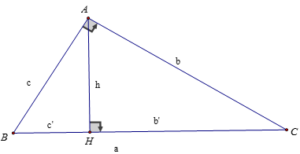
    Cho ΔABC, góc A bằng 90⁰, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:

        + BH = c’ được gọi là hình chiếu của AB xuống BC

        + CH = b’ được gọi là hình chiếu của AC xuống BC

    Khi đó, ta có:

    1) AB² = BH.BC hay c² = a.c’

    AC² = CH.BC hay b² = a.b’

    2) AH² = CH.BH hay h² = b’.c’

    3) AB.AC = AH.BC hay b.c = a.h

    5) AB² + AC² = BC² hay b² + c² = a² (Định lý Pytago)

1. Định nghĩa

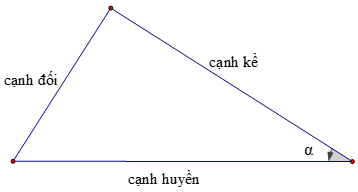
2. Định lí

    Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.

3. Một số hệ thức cơ bản

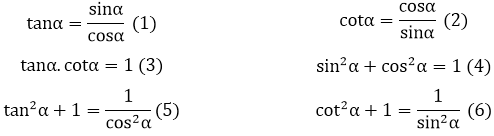
4. So sánh các tỉ số lượng giác

    a) Cho α,β là hai góc nhọn. Nếu α < β thì

    * sinα < sinβ; tanα < tanβ

    *cosα > cosβ; cotα > cotβ

    b) sinα < tanα; cosα < cotα

1. Các hệ thức

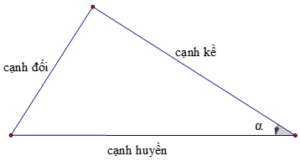
    Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

    a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề

    b) Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề

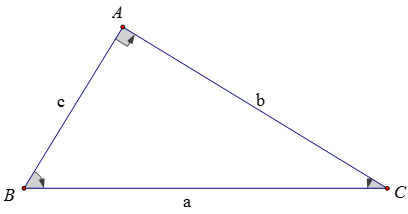
    b = a.sinB = a.cosC

    c = a.sinC = a.cosB

    b = c.tanB = c.cotC

    c = b.tanB = b.cotC

2. Giải tam giác vuông

    Là tìm tất cả các yếu tố còn lại của một tam giác vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông)

Chuyên đề Toán 9: đầy đủ Lý thuyết và các dạng bài tập có đáp án khác: