Lý thuyết Cực trị hàm số lớp 12 (hay, chi tiết) – Tổng hợp lý thuyết Toán 12 hay, chi tiết đầy đủ Giải tích và Hình học giúp học sinh nắm vững kiến thức trọng tâm Toán lớp 12.-Lý thuyết Cực trị hàm số lớp 12 (hay, chi tiết)
Lý thuyết Cực trị hàm số lớp 12 (hay, chi tiết)
Lý thuyết Cực trị hàm số
Bài giảng: Bài 2: Cực trị của hàm số – Thầy Trần Thế Mạnh (Giáo viên Meraki Center)
1. Định nghĩa:
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là -∝; b là +∝) và điểm xo ∈ (a; b) .
– Nếu tồn tại số h > 0 sao cho f(x) < f(xo) với mọi x ∈ (xo – h; xo + h) và x ≠ xo thì ta nói hàm số f(x) đạt cực đại tại xo .
– Nếu tồn tại số h > 0 sao cho f(x) > f(xo) với mọi x ∈ (xo – h; xo + h) và x ≠ xo thì ta nói hàm số f(x) đạt cực tiểu tại xo .
2. Điều kiện đủ để hàm số có cực trị:
Giả sử hàm số y = f(x) liên tục trên K = (xo – h; xo + h) và có đạo hàm trên K hoặc trên K {xo}, với h > 0 .
– Nếu f'(x) > 0 trên khoảng (xo – h; xo) và f'(x) < 0 trên (xo; xo + h) thì xo là một điểm cực đại của hàm số f(x).
– Nếu f'(x) < 0 trên khoảng (xo – h; xo) và f'(x) > 0 trên (xo; xo + h) thì xo là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
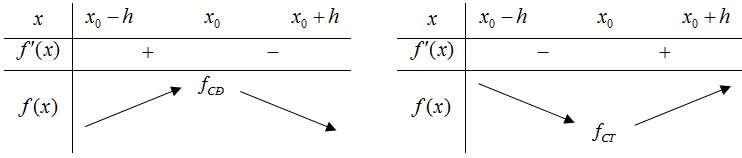
* Chú ý.
– Nếu hàm số y = f(x) đạt cực đại (cực tiểu) tại xo thì xo được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(xo) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCĐ(fCT) , còn điểm M(xo; f(xo)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
– Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
1. Quy tắc tìm cực trị của hàm số
– Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x) . Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
– Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x) và ký hiệu xi (i = 1; 2; 3;…) là các nghiệm của nó.
Bước 3. Tính f”(x) và f”(xi).
Bước 4. Dựa vào dấu của f”(xi) suy ra tính chất cực trị của điểm xi.
2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0)
Ta có y’= 3ax2 + 2bx + c
– Đồ thị hàm số có hai điểm cực trị khi phương trình y’ = 0 có hai nghiệm phân biệt ⇔ b2 – 3ac > 0. Khi đó đường thẳng qua hai điểm cực trị đó là : 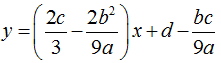 .
.
– Bấm máy tính tìm ra đường thẳng đi qua hai điểm cực trị :
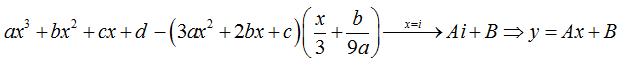
Hoặc sử dụng công thức 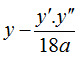 .
.
– Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc ba là:
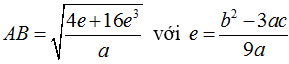
3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
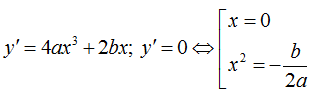
(C) có ba điểm cực trị y’ = 0 có 3 nghiệm phân biệt 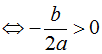 .
.
Khi đó ba điểm cực trị là: 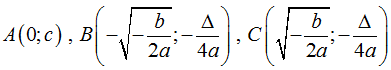 với Δ = b2 – 4ac
với Δ = b2 – 4ac
Độ dài các đoạn thẳng: 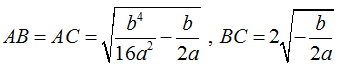 .
.
Các kết quả cần ghi nhớ:
– ΔABC vuông cân ⇔ BC2 = AB2 + AC2
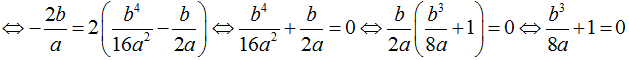
– ΔABC đều ⇔ BC2 = AB2
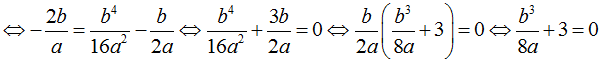
– 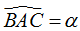 , ta có:
, ta có: 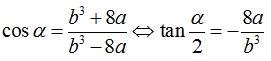
– 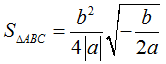
– Bán kính đường tròn ngoại tiếp ΔABC là 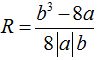
– Bán kính đường tròn nội tiếp ΔABC là 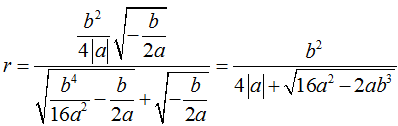
– Phương trình đường tròn ngoại tiếp ΔABC là: 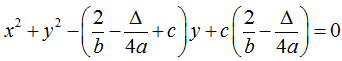
Ví dụ 1: Tìm đường thẳng đi qua hai điểm cực trị của đồ thị hàm số: y = x3 + 3x2 – x + 2
Lời giải:
Bấm máy tính: MODE 2
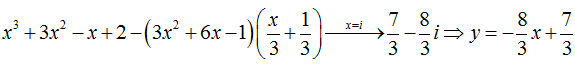
Ví dụ 2: Tìm đường thẳng đi qua hai điểm cực trị ( nếu có ) của đồ thị hàm số: y = x3 – 3x2 + m2x + m
Lời giải:
Bấm máy tính: MODE 2
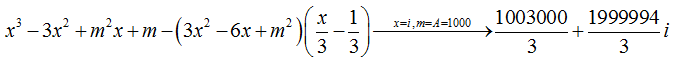
Ta có:
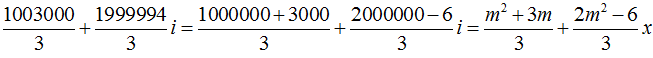
Vậy đường thẳng cần tìm:
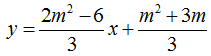
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:

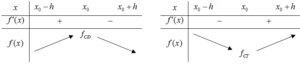
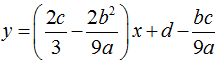

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn