Lý thuyết Đa thức lớp 7 (hay, chi tiết) – Tổng hợp lý thuyết Toán lớp 7 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 7.-Lý thuyết Đa thức lớp 7 (hay, chi tiết)
Lý thuyết Đa thức lớp 7 (hay, chi tiết)
Bài viết Lý thuyết Đa thức lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Đa thức.
Lý thuyết Đa thức lớp 7 (hay, chi tiết)
1. Đa thức
Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Ví dụ 1: x3 – 3, xyz – ax2 + by, a(3xy + 7x) là các đa thức.
Ví dụ 2: Đa thức 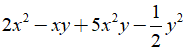 có thể viết lại như sau:
có thể viết lại như sau:
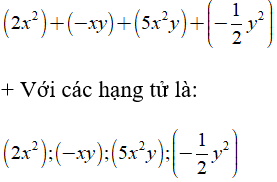
Chú ý: Mỗi đơn thức được coi là một đa thức.
2. Thu gọn đa thức
Đưa đa thức về dạng thu gọn (không còn hai hạng tử nào đồng dạng).
• Bước 1: Nhóm các đơn thức đồng dạng với nhau.
• Bước 2: Cộng, trừ các đơn thức đồng dạng trong từng nhóm.
Ví dụ: Thu gọn đa thức
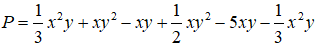
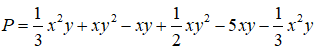
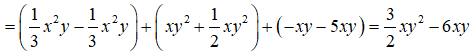
3. Bậc của đa thức
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó
Ví dụ: Đa thức x6 – 2y5 + x4y5 + 1 có bậc là 9; đa thức 3xy2/2 có bậc là 3.
Chú ý:
+ Số 0 cũng được gọi là đa thức không và nó không có bậc.
+ Khi tìm bậc của một đa thức, trước hết ta phải thu gọn đa thức đó.
Ví dụ 2: Thu gọn các đa thức và tìm bậc của đa thức
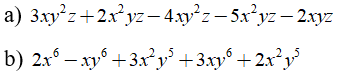
Hướng dẫn giải:
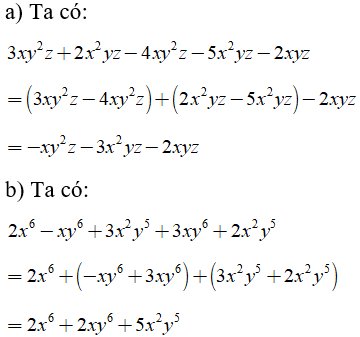
Bài 1: Tìm bậc của đa thức
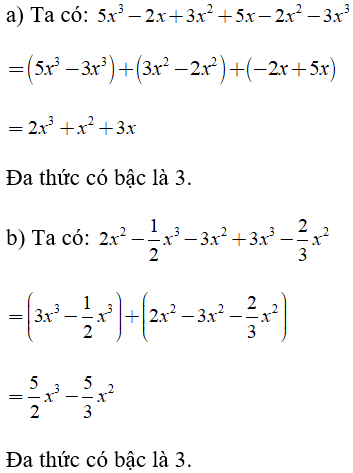
Lời giải:
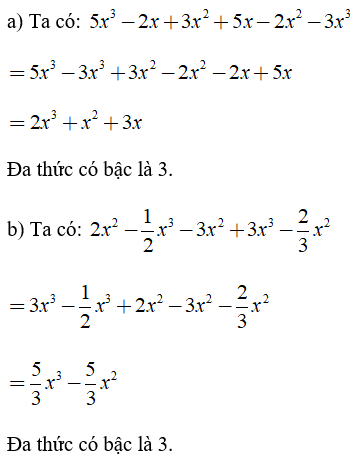 ẻ
ẻ
Bài 2: Tính giá trị của các đa thức
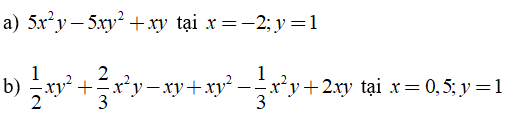
Lời giải:
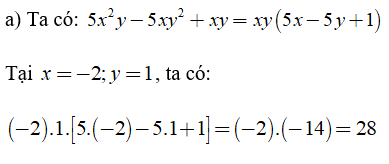
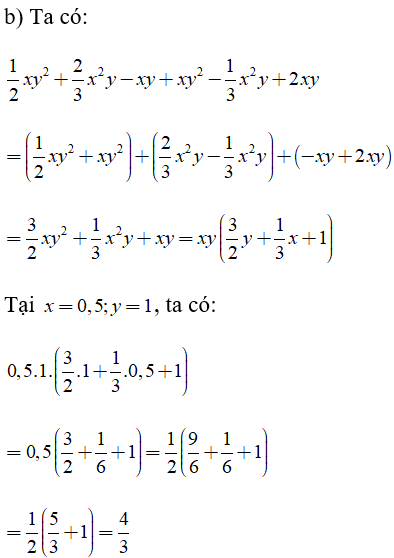
Bài 1. Tìm bậc của đa thức:
a) 2x3 – x + 2x2 + 6x – 2x2 – 3x3;
b) x2-12×3-x2+3×3-23×2.
Hướng dẫn giải:
a) 2x3 – x + 2x2 + 6x – 2x2 – 3x3
= (2x3 – 3x3) + (2x2 – 2x2) + (6x – x)
= −x3 + 5
Vậy đa thức có bậc là 3.
b) x2-12×3-x2+3×3-23×2
=(3×3-12×3)+(x2-x2-23×2)
=52×3-23×2
Vậy đa thức có bậc là 3.
Bài 2. Cho đa thức B=-2xy2+13x2y-x-13x2y+xy2+x-4x2y
a) Thu gọn B;
b) Tìm bậc của B;
c) Tính giá trị của B tại x = 1; y = 2.
Hướng dẫn giải:
a) Ta có:
B=-2xy2+13x2y-x-13x2y+xy2+x-4x2y
=(-2xy2+xy2)+(13x2y-13x2y)+(-x+x)-4x2y
= (−2 + 1)xy2 + 0 + 0 – 4x2y
= −xy2 – 4x2y
b) Bậc của đa thức B là 3
c) Thay x = 1 và y = 2 vào đa thức B, ta được:
B = −1.22 – 4.12.2
= −4 – 8 = −12.
Bài 3. Thu gọn đa thức sau:
a) M=y2-2y+12y2+5y-y2;
b) N=13x2y+xy2-xy+12xy2-5xy-13x2y.
Hướng dẫn giải:
a) M=y2-2y+12y2+5y-y2
=(y2+12y2-y2)+(-2y+5y)
=(1+12-1)y2+(-2+5)y
=12y2+3y
b) N=13x2y+xy2-xy+12xy2-5xy-13x2y
=(13x2y-13x2y)+(xy2+12xy2)+(-xy-5xy)
=0+(1+12)xy2+(-1-5)xy
=32xy2-6xy
Bài 4. Thu gọn đa thức sau:
a) A=2×2+x-12×2+5x;
b) B=5xy+12x2y-23xy+2x2y.
Hướng dẫn giải:
a) A=2×2+x-12×2+5x
=(2×2-12×2)+(x+5x)
=(2-12)x2+(1+5)x
=32×2+6x.
b) B=5xy+12x2y-23xy+2x2y
=(5xy-23xy)+(12x2y+2x2y)
=(5-23)xy+(12+2)x2y
=133xy+52x2y.
5. Thu gọn và chỉ ra bậc của đa thức:
A = 2x3 – 2xy + x2 + 5xy – x3 – x2.
Hướng dẫn giải:
A = 2x3 – 2xy + x2 + 5xy – x3 – x2
= (2x3 – x3) + (x2 – x2) + (5xy – 2xy)
= x3 + 3xy
Vậy bậc của đa thức A là 3.
Bài 6. Cho đa thức A = 3x2 – 2x + x2 + 1 + 2x.
a) Thu gọn A;
b) Tính giá trị của A tại x = 1.
Bài 7. Cho đa thức M = ab + 3a2b + 2a2 – 2ab – 3a2b.
a) Thu gọn M;
b) Tìm bậc của M và tính giá trị của M tại a = 2; b = 1.
Bài 8. Cho đa thức M = 2x2 – 3x2 + 1 – x2 + 5x2 – 2.
a) Thu gọn M.
b) Tìm bậc của M.
c) Tính giá trị của M tại x = 2.
Bài 9. Cho đa thức P=2xy+12x2y2-xy-12x2y2+y-1.
a) Thu gọn P.
b) Tính giá trị của P tại x = 0,1; y = −2.
Bài 10. Cho a, b, c là những hằng số thỏa mãn a + b + c = 2006. Tính giá trịc của đa thức sau:
a) A = ax2y2 + bx2y + cxy2 tại x = 1; y = 1.
b) B = ax2y2 – bx4y + cxy4 tại x = 1; y = −1.
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:
Lời giải bài tập lớp 7 sách mới:

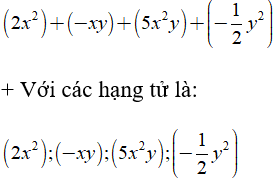

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn