Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét lớp 8 (hay, chi tiết) – Tổng hợp Lý thuyết Toán 8 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 8.-Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét lớp 8 (hay, chi tiết)
Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét lớp 8 (hay, chi tiết)
Bài viết Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét.
Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét
Bài giảng: Bài 2: Định lí đảo và hệ quả của định lí Ta-lét – Cô Vương Thị Hạnh (Giáo viên VietJack)
1. Định lý đảo
Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
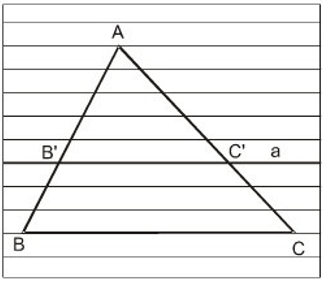
Tổng quát: Δ ABC, B’ ∈ AB, C’ ∈ AC; AB’/BB’ = AC’/C’C
Suy ra: B’C’//BC.
Ví dụ: Trong Δ ABC có AB = 6cm, AC = 9cm. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 2cm, AC’ = 3cm. Chứng minh B’C’//BC.
Lời giải:
Trong Δ ABC, B’ ∈ AB, C’ ∈ AC.
Ta có
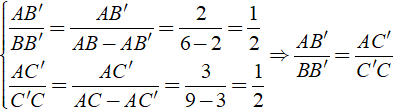
Suy ra: B’C’//BC.
2. Hệ quả của định lý Ta – lét
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
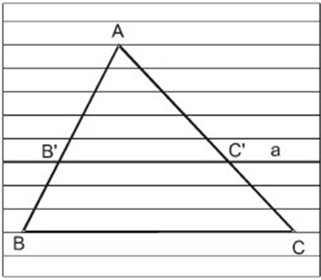
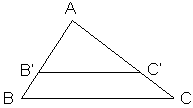
Tổng quát : Δ ABC, B’C’//BC; B’ ∈ AB, C’ ∈ AC
Ta có: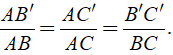
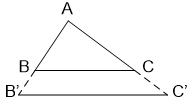
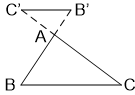
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.
Ví dụ: Trong Δ ABC có AB = 8cm và B’C’//BC. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 2cm, AC’ = 3cm. Tính độ dài cạnh AC.
Lời giải:
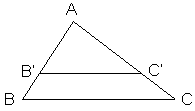
Áp dụng hệ quả trên ta có: Δ ABC, B’C’//BC; B’ ∈ AB, C’ ∈ AC
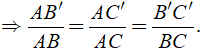
Khi đó ta có: AB’/AB = AC’/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )
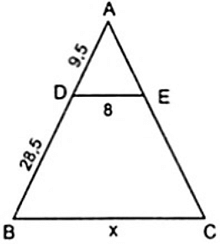
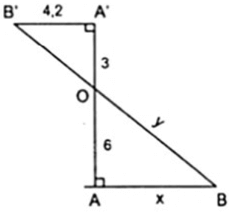
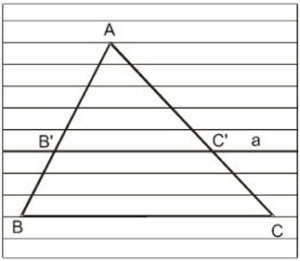
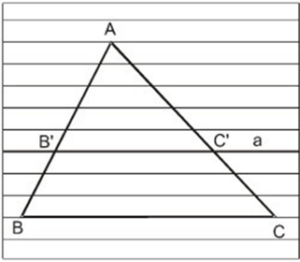
Bài 1: Tính độ dài x, y trong các hình bên
Lời giải:
a) Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = (8.28,5)/9,5 = 456/19 ≈ 31,58
b) Ta có: A’B’//AB vì cùng vuông góc AA’
Áp dụng hệ quả của định lí Ta – lét ta có:
A’B’//AB ⇒ AB/A’B’ = AO/A’O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
OB2 = AB2 + OA2 ⇒ y = √(8,42 + 62) ≈ 10,32
Bài 2: Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
Lời giải:
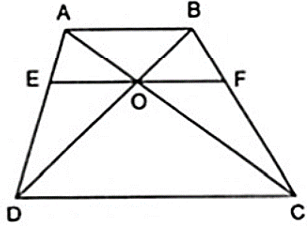
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
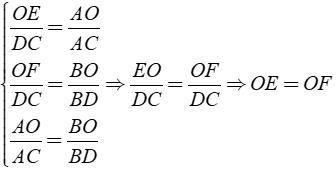
Điều phải chứng minh.
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

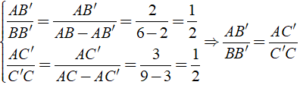

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn