Lý thuyết Hai đường thẳng vuông góc lớp 7 (hay, chi tiết)

Bài viết Lý thuyết Hai đường thẳng vuông góc lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Hai đường thẳng vuông góc.

Lý thuyết Hai đường thẳng vuông góc lớp 7 (hay, chi tiết)

1. Định nghĩa hai đường thẳng vuông góc

Hai đường thẳng vuông góc là hai đường thẳng cắt nhau và một trong các góc tạo thành là góc vuông

Ví dụ: AB ⊥ CD (tại O) ⇒ ∠AOC = 90^o

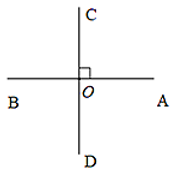
Tính duy nhất của một đường vuông góc

Qua một điểm cho trước, có một và chỉ một đường thẳng vuông góc với một đường thẳng cho trước.

Ví dụ: Cho 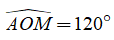. Vẽ các tia OB, OC nằm trong góc 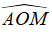sao cho OB ⊥ OA , OC ⊥ OM. Tính số đo góc BOC?

Hướng dẫn giải:

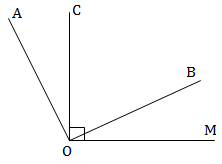
OB nằm giữa OA, OM

2. Cách vẽ hai đường thẳng vuông góc

   + Ta thường dung eke và thước kẻ để vẽ hai đường thẳng vuông góc

   + Ta thừa nhận tính chất sau:

Tính chất : Có một và chỉ một đường thẳng a’ đi qua điểm O cho trước và vuông góc với đường thẳng a cho trước

Trường hợp điểm O cho trước nằm trên đường thẳng a.

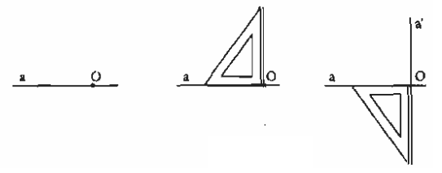
Trường hợp điểm O cho trước nằm ngoài đường thẳng

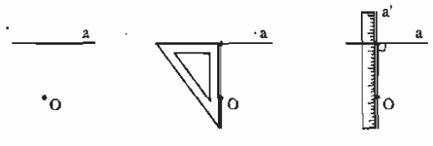
Ví dụ: Cho góc xOy tù, ở miền trong góc ấy dựng các tia Oz và Ot sao cho Oz vuông góc với Ox, Ot vuông góc với Oy. Tính tổng số đo của hai góc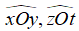

Hướng dẫn giải:

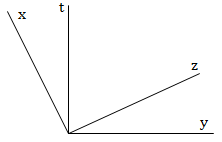
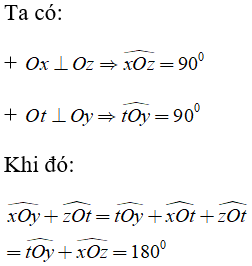
3. Đường trung trực của đoạn thẳng

Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng ấy tại trung điểm của nó

Ví dụ:

xy là đường trung trực của đoạn AB

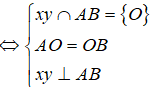
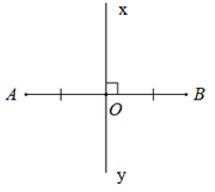
Chú ý: Kí hiệu xy ∩ AB = {O} đọc là xy cắt AB tại O

Bài 1: Chứng tỏ hai tia phân giác của hai góc kề bù vuông góc với nhau

Lời giải:

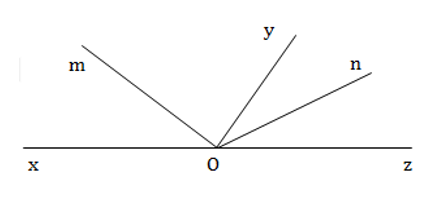
Gọi 2 góc kề bù là ∠xOy và ∠yOz, có lần lượt hai tia phân giác là Om và On

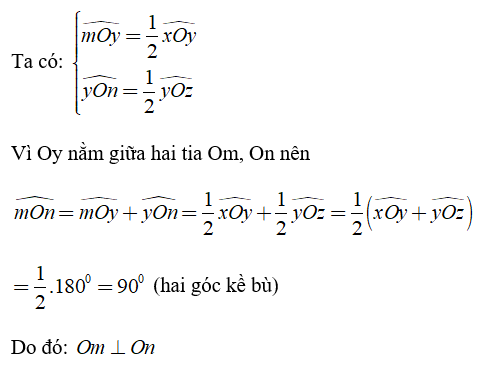
Vậy hai tia phân giác của hai góc kề bù vuông góc với nhau.

Bài 2: Cho góc tù AOB. Trong đó dựng hai tia OC, OD theo thứ tự vuông góc với OA, OB.

a) So sánh các góc ∠AOD và ∠BOC

b) Gọi OM là tia phân giác của góc COD. Xét xem tia OM có phải là tia phân giác của góc AOB hay không?

Lời giải:

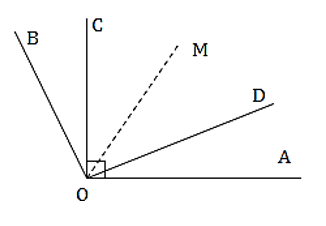
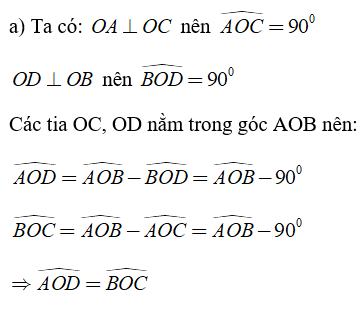
b) Vì ∠AOC < ∠AOB (góc vuông nhỏ hơn góc tù)

⇒ OC nằm giữa hai tia OA và OB

∠BOD < ∠AOB (góc vuông nhỏ hơn góc tù)

⇒ OD nằm giữa hai tia OA và OB

⇒ OD và OC nằm giữa hai tia OA và OB

⇒ OM là tia phân giác góc COD sẽ nằm giữa tia OA và OB

Mặt khác: OM là phân giác góc COD nên ∠MOC = ∠MOD

Theo chứng minh trên, ta có:

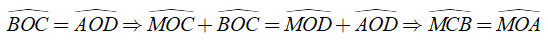
Khi đó: OM là tia phân giác AOB.

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:

Lời giải bài tập lớp 7 sách mới:

---