Lý thuyết Hai mặt phẳng song song lớp 11 (hay, chi tiết)

Bài viết Lý thuyết Hai mặt phẳng song song lớp 11 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Hai mặt phẳng song song.

Lý thuyết Hai mặt phẳng song song

Bài giảng: Bài 4: Hai mặt phẳng song song – Thầy Lê Thành Đạt (Giáo viên Meraki Center)

1. Vị trí tương đối của hai mặt phẳng phân biệt

    Cho 2 mặt phẳng (P) và (Q). Căn cứ vào số đường thẳng chung của 2 mặt phẳng ta có ba trường hợp sau:

a. Hai mặt phẳng (P) và (Q) không có đường thẳng chung, tức là:

        (P) ⋂ (Q) = ∅ ⇔ (P) // (Q).

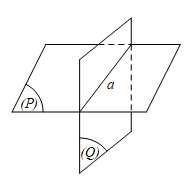
b. Hai mặt phẳng (P) và (Q) chỉ có một đường thẳng chung, tức là:

        (P) ⋂ (Q) = a ⇔ (P) cắt (Q).

c. Hai mặt phẳng (P) và (Q) có 2 đường thẳng chung phân biệt, tức là:

        (P) ⋂ (Q) = {a, b} ⇔ (P) ≡ (Q).

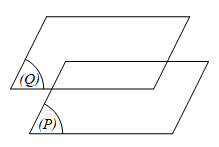
        (P) ⋂ (Q) = ∅ ⇔ (P) // (Q).

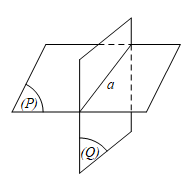
        (P) ⋂ (Q) = a ⇔ (P) cắt (Q).

        (P) ⋂ (Q) = {a, b} ⇔ (P) ≡ (Q).

2. Điều kiện để hai mặt phẳng song song

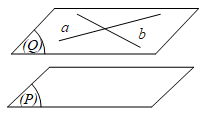
Định lí 1: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P) song song (Q).

Tức là: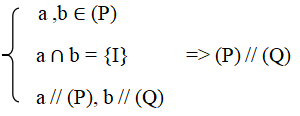

3. Tính chất

Tính chất 1: Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó.

Tức là: O ∉ (P) ⇒ ∃! (Q):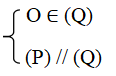

Cách dựng:

    + Trong (P) dựng a, b cắt nhau.

    + Qua O dựng a₁ // a, b₁ // b.

    + Mặt phẳng (a₁, b₁) là mặt phẳng qua O và song song với (P).

Hệ quả 1: Nếu đường thẳng a song song với mặt phẳng (Q) thì qua a có một và chỉ một mặt phẳng (P) song song với (Q).

Hệ quả 2: Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau.

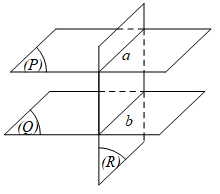
Tính chất 2: Nếu hai mặt phẳng (P) và (Q) song song thì mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.

Tức là: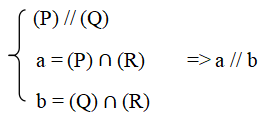

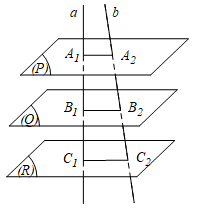
Định lí Ta – lét trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỷ lệ.

Tức là:

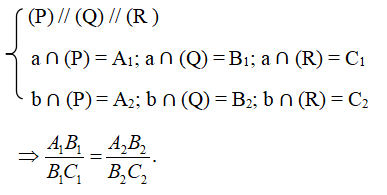
4. Hình lăng trụ và hình hộp

Định nghĩa hình lăng trụ: Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song gọi là hai đáy và tất cả các cạnh không thuộc hai cạnh đáy đều song song với nhau.

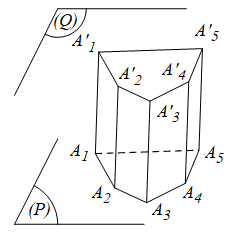
Trong đó:

    + Các mặt khác với hai đáy gọi là các mặt bên của hình lăng trụ.

    + Cạnh chung của hai mặt bên gọi là cạnh bên của hình lăng trụ.

    + Tùy theo đa giác đáy, ta có hình lăng trụ tam giác, lăng trụ tứ giác …

Từ định nghĩa của hình lăng trụ, ta lần lượt suy ra các tính chất sau:

a. Các cạnh bên song song và bằng nhau.

b. Các mặt bên và các mặt chéo là những hình bình hành.

c. Hai đáy là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Định nghĩa hình hộp: Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.

    a. Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật.

    b. Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương.

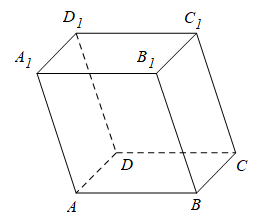
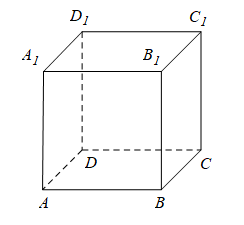
Chú ý: Các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.

5. Hình chóp cụt

Định nghĩa: Cho hình chóp S.A₁A₂…A_n. Một mặt phẳng (P) song song với mặt phẳng chứa đa giác đáy cắt các cạnh SA₁, SA₂,…, SA_n theo thứ tự tại A’₁, A’₂,…, A’_n. Hình tạo bởi thiết diện A’₁A’₂…A’_n và đáy A₁A₂…A_n của hình chóp cùng với các mặt bên A₁A₂A’₂A’₁, A₂A₃A’₃A’₂,…, A_nA₁A’₁A’_n gọi là một hình chóp cụt.

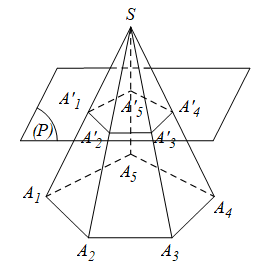
Trong đó:

    + Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện gọi là đáy nhỏ của hình chóp cụt.

    + Các mặt còn lại gọi là các mặt bên của hình chóp cụt.

    + Cạnh chung của hai mặt bên kề nhau như A₁A’₁, A₂A’₂,…, A_nA’_n gọi là cạnh bên của hình chóp cụt.

Tùy theo đáy là tam giác, tứ giác, ngũ giác,… ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chụp cụt ngũ giác,…

Tính chất: Với hình chóp cụt, ta có các tính chất sau:

    1. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.

    2. Các mặt bên của hình chóp cụt là các hình thang.

    3. Các cạnh bên của hình chóp cụt đồng quy tại một điểm.

Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác: