Lý thuyết Hàm số bậc hai lớp 10 (hay, chi tiết) – Tổng hợp lý thuyết Toán 10 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm môn Toán 10.-Lý thuyết Hàm số bậc hai lớp 10 (hay, chi tiết)
Lý thuyết Hàm số bậc hai lớp 10 (hay, chi tiết)
Bài viết Lý thuyết Hàm số bậc hai lớp 10 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Hàm số bậc hai.
Lý thuyết Hàm số bậc hai
Bài giảng: Bài 3: Hàm số bậc hai – Thầy Lê Thành Đạt (Giáo viên Meraki Center)
Hàm số bậc hai được cho bởi công thức
y = ax2 + bx + c (a ≠ 0).
Tập xác định của hàm số này là D = R
Hàm số y = ax2 (a ≠ 0) đã học ở lớp 9 là một trường hợp riêng của hàm số này.
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm I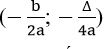 , có trục đối xứng là đường thẳng x = –
, có trục đối xứng là đường thẳng x = –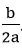 . Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
. Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
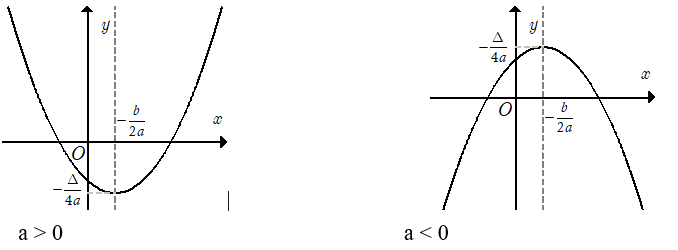
Cách vẽ
Để vẽ parabol y = ax2 + bx + c (a≠0) ta thực hiện các bước
1) Xác định tọa độ của đỉnh I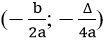
2) Vẽ trục đối xứng x = –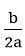 .
.
3) Xác định tọa độ các giao điểm của parabol với trục tung (điểm (0; c)) và trục hoành (nếu có).
Xác định thêm một số điểm thuộc đồ thị, chẳng hạn điểm đối xứng với điểm (0; c) qua trục đối xứng của parabol, để vẽ đồ thị chính xác hơn.
4) Vẽ parabol.
Khi vẽ parabol cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới).
II. CHIỀU BIẾN THIÊN CỦA HÀM SỐ BẬC HAI
Dựa vào đồ thị hàm số y = ax2 + bx + c (a≠0) ta có bảng biến thiên của nó trong hai trường hợp a > 0 và a < 0 như sau
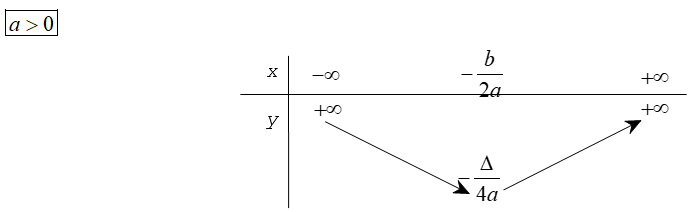
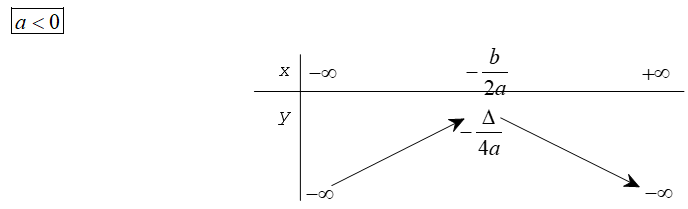
Từ đó, ta có định lí dưới đây
Định lí
Nếu a < 0 thì hàm số y = ax2 + bx + c nghịch biến trên khoảng (–∞; –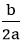 ); đồng biến trên khoảng (-
); đồng biến trên khoảng (-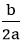 ; +∞).
; +∞).
Nếu a > 0 thì hàm số y = ax2 + bx + c đồng biến trên khoảng (–∞; –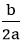 ) nghịch biến trên khoảng (-
) nghịch biến trên khoảng (-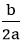 ; +∞).
; +∞).
Xem thêm các dạng bài tập Toán 10 có đáp án hay khác:
Lời giải bài tập lớp 10 sách mới:

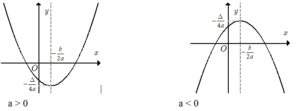

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn