Lý thuyết Hệ tọa độ trong không gian lớp 12 (hay, chi tiết)

---

---

Bài viết Lý thuyết Hệ tọa độ trong không gian lớp 12 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Hệ tọa độ trong không gian.

Lý thuyết Hệ tọa độ trong không gian

Bài giảng: Bài 1 : Hệ tọa độ trong không gian – Thầy Trần Thế Mạnh (Giáo viên VietJack)

1. Hệ trục tọa độ trong không gian

    Trong không gian, xét ba trục tọa độ Ox, Oy, Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi i→, j→, k→ là các vectơ đơn vị, tương ứng trên các trục Ox, Oy, Oz. Hệ ba trục như vậy gọi là hệ trục tọa độ vuông góc trong không gian.

    Chú ý: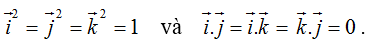

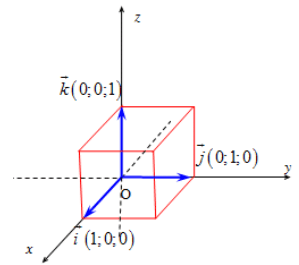
2. Tọa độ của vectơ

    a) Định nghĩa: u→ = (x; y; z) ⇔ k→ = xi→ + yj→ + zk→

    b) Tính chất: Cho a→ = (a₁; a₂; a₃), b→ = (b₁; b₂; b₃), k ∈ R

    • a→ ± b→ = (a₁ ± b₁; a₂ ± b₂; a₃ ± b₃; )

    • ka→ = (ka₁; ka₂; ka₃)

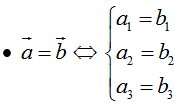
    • 0→ = (0; 0; 0), i→ = (1; 0; 0), j→ = (0; 1; 0), k→ = (0; 0; 1)

    • a→ cùng phương b→ (b→ ≠ 0→) ⇔ a→ = kb→ (k ∈ R)

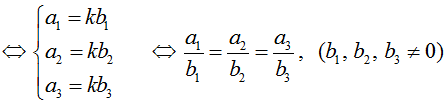
    • a→.b→ = a₁.b₁ + a₂.b₂ + a₃.b₃

    • a→ ⊥ b→ ⇔ a₁b₁ + a₂b₂ + a₃b₃ = 0

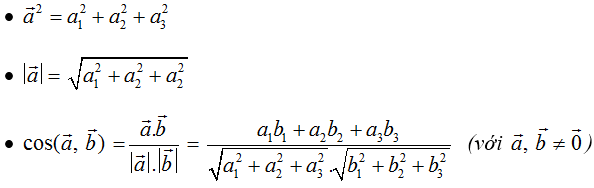
3. Tọa độ của điểm

    a) Định nghĩa: M(x; y; z) ⇔ OM→ = x.i→ + y.j→ + z.k→ (x : hoành độ, y : tung độ, z : cao độ)

    Chú ý: • M ∈ (Oxy) ⇔ z = 0; M ∈ (Oyz) ⇔ x = 0; M ∈ (Oxz) ⇔ y = 0

    • M ∈ Ox ⇔ y = z = 0; M ∈ Oy ⇔ x = z = 0; M ∈ Oz ⇔ x = y = 0 .

    b) Tính chất: Cho A(x_A; y_A; z_A), B(x_B; y_B; z_B)

    • AB→ = (x_B – x_A; y_B – y_A; z_B – z_A)

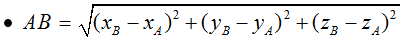
    • Toạ độ trung điểm của đoạn thẳng AB:

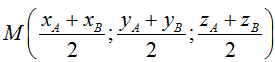
    • Toạ độ trọng tâm G của tam giác ABC:

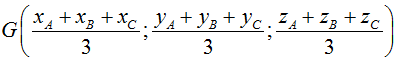
    • Toạ độ trọng tâm G của tứ diện ABCD:

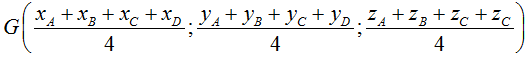
4. Tích có hướng của hai vectơ

    a) Định nghĩa: Trong không gian Oxyz cho hai vectơ a→ = (a₁; a₂; a₃), b→ = (b₁; b₂; b₃). Tích có hướng của hai vectơ a→ và b→ kí hiệu là [a→, b→], được xác định bởi

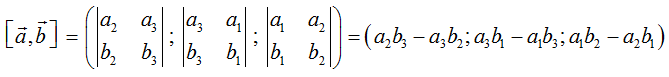
    Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

    b) Tính chất:

    • [a→, b→] ⊥ a→; [a→, b→] ⊥ b→

    • [a→, b→] = -[b→, a→]

    • [i→, j→] = k→; [j→, k→] = i→; [k→, i→] = j→

    • |[a→, b→]| = |a→|.|b→|.sin(a→, b→) (Chương trình nâng cao)

    • a→, b→ cùng phương ⇔ [a→, b→] = 0→ (chứng minh 3 điểm thẳng hàng)

    c) Ứng dụng của tích có hướng: (Chương trình nâng cao)

    • Điều kiện đồng phẳng của ba vectơ: a→, b→ và c→ đồng phẳng ⇔ [a→, b→].c→ = 0

    • Diện tích hình bình hành ABCD: S_ABCD = |[AB→], AD→|

    • Diện tích tam giác ABC: S_ABC = 1/2 |[AB→], AC→|

    • Thể tích khối hộp ABCDA’B’C’D’ : V_{ABCD.A’B’C’D’} = |[AB→, AD→].AA’→|

    • Thể tích tứ diện ABCD: V_ABCD = 1/6 |[AB→, AC→].AD→|

    Chú ý:

    – Tích vô hướng của hai vectơ thường sử dụng để chứng minh hai đường thẳng vuông góc, tính góc giữa hai đường thẳng.

    – Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.

5. Phương trình mặt cầu

    a) Định nghĩa:

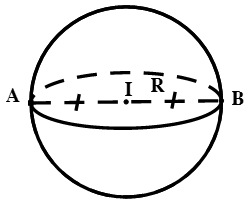
    Cho điểm I cố định và một số thực dương R. Tập hợp tất cả những điểm M trong không gian cách I một khoảng R được gọi là mặt cầu tâm I, bán kính R.

    Kí hiệu: S(I; R) ⇔ S(I; R) = {M|IM = R}

    b) Vị trí tương đối giữa mặt cầu và mặt phẳng :

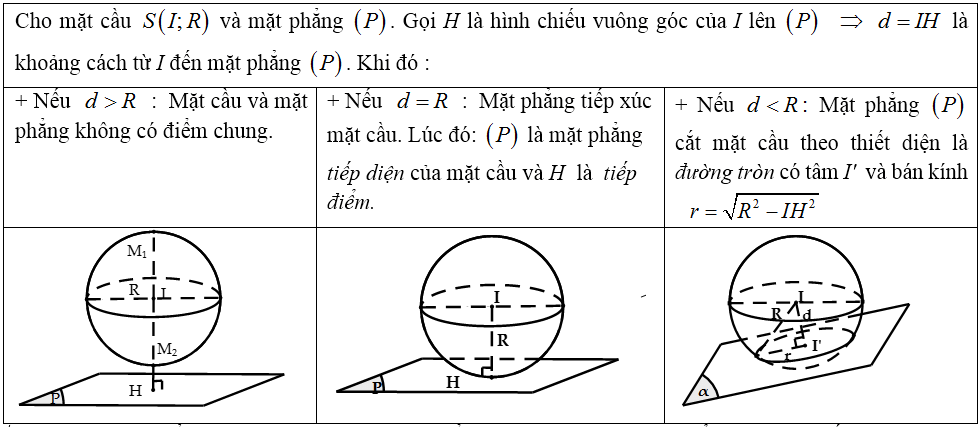
    Lưu ý: Khi mặt phẳng (P) đi qua tâm I thì mặt phẳng (P) được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.

    c) Vị trí tương đối giữa mặt cầu và đường thẳng :

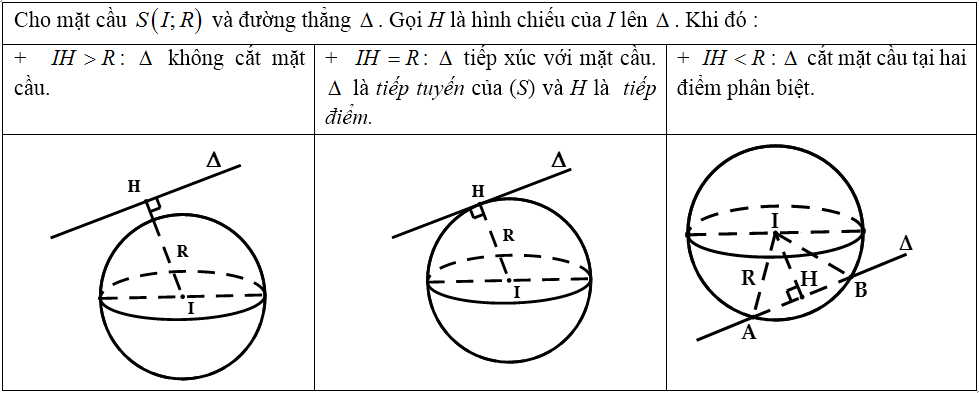
    * Lưu ý: Trong trường hợp Δ cắt (S) tại 2 điểm A, B thì bán kính R của (S) được tính như sau:

        + Xác định: d(I; Δ) = IH

        + Lúc đó: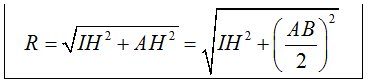

    ĐƯỜNG TRÒN TRONG KHÔNG GIAN OXYZ

    * Đường tròn (C) trong không gian Oxyz, được xem là giao tuyến của (S) và mặt phẳng .

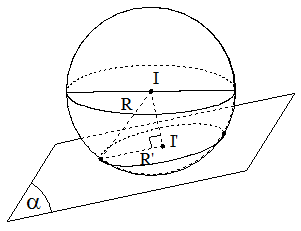
    (S): x² + y² + z² – 2ax -2by – 2cz + d = 0

    (α): Ax + By + Cz + D = 0

    * Xác định tâm I’ và bán kính R’ của (C).

        + Tâm I’ = d ∩ (α) .

    Trong đó d là đường thẳng đi qua I và vuông góc với mp(α)

        + Bán kính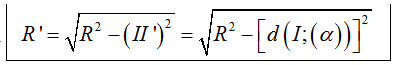

    d) Điều kiện tiếp xúc : Cho mặt cầu (S) tâm I, bán kính R.

        + Đường thẳng Δ là tiếp tuyến của (S) ⇔ d(I; Δ) = R

        + Mặt phẳng (α) là tiếp diện của (S) ⇔ d(I;(α)) = R

    * Lưu ý: Tìm tiếp điểm M_o(x_o; y_o; z_o) .

    Sử dụng tính chất :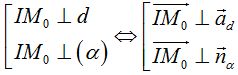

Dạng 1: VIẾT PHƯƠNG TRÌNH MẶT CẦU

    Phương pháp:

    * Cách 1: Bước 1: Xác định tâm I(a; b; c) .

    Bước 2: Xác định bán kính R của (S).

    Bước 3: Mặt cầu (S) có tâm I(a; b; c) và bán kính R.

    (S): (x – a)² + (y – b)² + (z – c)² = R²

    * Cách 2: Gọi phương trình (S): x² + y² + z² -2ax – 2by – 2cz + d = 0

    Phương trình (S) hoàn toàn xác định nếu biết được a, b, c, d. (a² + b² + c² – d > 0)

Bài 1: Viết phương trình mặt cầu (S), trong các trường hợp sau:

    a) (S) có tâm I(2; 2; -3) và bán kính R = 3 .

    b) (S) có tâm I(1; 2; 0) và (S) qua P(2; -2; 1).

    c) (S) có đường kính AB với A(1; 3; 1), B(-2; 0; 1).

Lời giải:

    a) Mặt cầu tâm I(2; 2; -3) và bán kính R = 3, có phương trình:

    (S): (x – 2)² + (y – 2)² + (z + 3)² = 9

    b) Ta có: IP→ = (1; -4; 1) ⇒ IP = 3√2.

    Mặt cầu tâm I(1; 2; 0) và bán kính R = IP = 3√2 , có phương trình:

    (S): (x – 1)² + (y – 2)² + z² = 18

    c) Ta có: AB→ = (-3; -3; 0) ⇒ AB = 3√2.

    Gọi I là trung điểm AB ⇒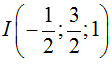

    Mặt cầu tâm 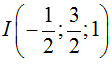và bán kính 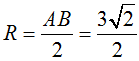, có phương trình:

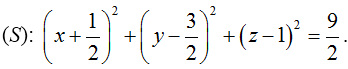
Bài 2:Viết phương trình mặt cầu (S) , trong các trường hợp sau:

    a) (S) qua A(3; 1; 0), B(5; 5; 0) và tâm I thuộc trục Õ.

    b) (S) có tâm O và tiếp xúc mặt phẳng (α): 16x – 15y – 12z + 75 = 0.

    c) (S) có tâm I(-1; 2; 0) và có một tiếp tuyến là đường thẳng

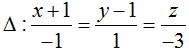
Lời giải:

    a) Gọi I(a; 0; 0) ∈ Ox. Ta có : IA→ = (3-a; 1; 0), IB→ = (5-a; 5; 0).

    Do (S) đi qua A, B ⇔ IA = IB 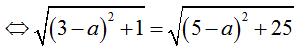⇔ 4a = 40 ⇔ a = 10

    ⇒ I(10; 0; 0) và IA = 5√2.

    Mặt cầu tâm I(10; 0; 0) và bán kính R = 5√2, có phương trình (S) : (x – 10)² + y² + z² = 50

    b) Do (S) tiếp xúc với (α) ⇔ d(O,(α)) = R ⇔ R = 75/25 = 3

    Mặt cầu tâm O(0; 0; 0) và bán kính R = 3, có phương trình (S) : x² + y² + z² = 9

    c) Chọn A(-1; 1; 0) ∈ Δ ⇒ IA→ = (0; -1; 0).

    Đường thẳng Δ có một vectơ chỉ phương là u_Δ→ = (-1; 1; -3) . Ta có: [IA→, u_Δ→] = (3; 0; -1) .

    Do (S) tiếp xúc với Δ ⇔ d(I, Δ) = R .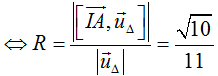

    Mặt cầu tâm I(-1; 2; 0) và bán kính R = √10/11 , có phương trình (S) :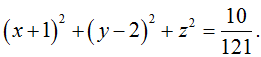

Dạng 2 : SỰ TƯƠNG GIAO VÀ SỰ TIẾP XÚC

    Phương pháp: * Các điều kiện tiếp xúc:

        + Đường thẳng Δ là tiếp tuyến của (S) ⇔ d(I; Δ) = R

        + Mặt phẳng (α) là tiếp diện của (S) ⇔ d(I; (α)) = R

    * Lưu ý các dạng toán liên quan như tìm tiếp điểm, tương giao.

Bài 1: Cho đường thẳng 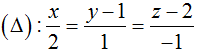và và mặt cầu (S): x² + y² + z² – 2x + 4z + 1 = 0 . Số điểm chung của (Δ) và (S) là :

    A. 0.         B.1.         C.2.         D.3.

Lời giải:

    Đường thẳng (Δ) đi qua M(0; 1; 2) và có một vectơ chỉ phương là u→ = (2; 1; -1)

    Mặt cầu (S) có tâm I(1; 0; -2) và bán kính R = 2

    Ta có MI→ = (1; -1; -4) và [u→, MI→] = (-5; 7; -3) ⇒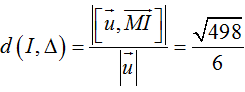

    Vì d(I,Δ) > R nên (Δ) không cắt mặt cầu (S)

Bài 2: Cho điểm I(1; -2; 3). Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:

    A. (x – 1)² + (y + 2)² + (z – 3)² = √10

    B. (x – 1)² + (y + 2)² + (z – 3)² = 10

    C. (x + 1)² + (y 2 2)² + (z + 3)² = 10

    D. (x – 1)² + (y + 2)² + (z – 3)² = 9

Lời giải:

    Gọi M là hình chiếu của I(1; -2; 3) lên Oy, ta có : M(0; -2; 0).

    IM→ (-1; 0; -3) ⇒ R = d(I,Oy) = IM = √10 là bán kính mặt cầu cần tìm.

    Phương trình mặt cầu là : (x – 1)² + (y + 2)² + (z – 3)² = 10

Lý thuyết và bài tập trắc nghiệm có đáp án và lời giải chi tiết Toán lớp 12 khác:

---

---

---