Lý thuyết Hình lăng trụ đứng lớp 8 (hay, chi tiết)

Bài viết Lý thuyết Hình lăng trụ đứng lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Hình lăng trụ đứng.

Lý thuyết Hình lăng trụ đứng

Bài giảng: Bài 4: Hình lăng trụ đứng – Cô Vương Thị Hạnh (Giáo viên Meraki Center)

1. Hình lăng trụ đứng

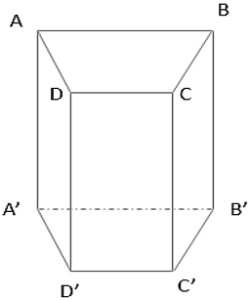
Hình vẽ dưới đây gọi là lăng trụ đứng.

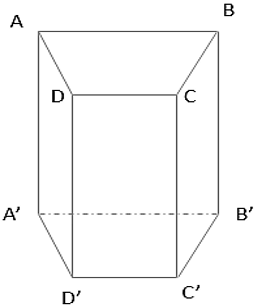
Trong hình lăng trụ đứng này:

+ A, B, C, D, A’, B’, C’, D’ là các đỉnh.

+ ABB’A’, BCC’B’,… là những hình chữ nhật, gọi là các mặt bên

+ AA’; BB’; CC’; DD’ song song với nhau và bằng nhau, chúng được gọi là các cạnh bên

+ Hai mặt ABCD và A’B’C’D’ là hai đáy. Hình lăng trụ trên có hai đáy là tứ giác nên gọi là lặng trụ tứ giác, kí hiệu : ABCD.A’B’C’D’

Chú ý:

– Hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.

– Các cạnh bên song song, bằng nhau và vuông góc với hai mặt phẳng đáy. Độ dài cạnh bên được gọi chiều cao của hình lăng trụ đứng.

– Các mặt bên là những hình chữ nhật và vuông góc với hai mặt phẳng đáy.

– Hình hộp chữ nhật, hình lập phương là những hình lăng trụ đứng.

– Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.

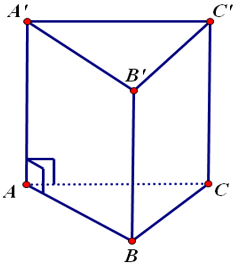
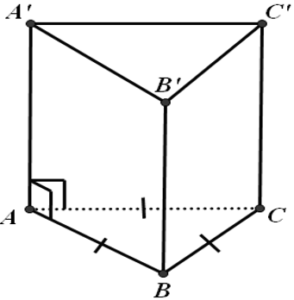
Ví dụ: Cho hình lưng trụ đứng sau:

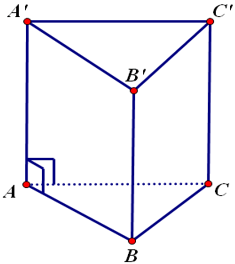
Hai mặt đáy ABC và A’B’C’ là hai tam giác bằng nhau (nằm trong hai mặt phẳng song song)

Các mặt bên A’C’CA, A’B’BA, B’C’CB là các hình chữ nhật.

2. Diện tích – Thể tích của hình lăng trụ đứng

a) Công thức diện tích xung quanh

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao:

S_xq = 2p.h    (p: nửa chu vi đáy, h: chiều cao)

b) Diện tích toàn phần

Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

S_tp = S_xq + 2S    (S: điện tích đáy)

c) Thể tích

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao:

V = S.h    (S: diện tích đáy, h: chiều cao)

d) Ví dụ

Ví dụ: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, AB = 4cm,AA’ = 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lặng trụ ABC.A’B’C’ ?

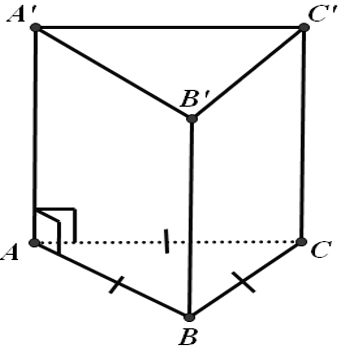
Lời giải:

Xét tam giác ABC có nửa chu vi của tam giác là:

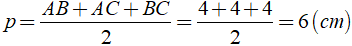
Khi đó ta có

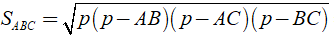
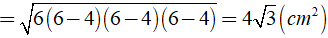
+ Diện tích xung quanh của hình lăng trụ S_xq = 2p.AA’ = 2.6.5 = 60( cm² )

+ Diện tích toàn phần của hình lăng trụ là S_tp = S_xq + 2S_ABC = 60 + 2.4√ 3 = 60 + 8√ 3 ( cm² )

+ Thể tích của hình lăng trụ là V = S.AA’ = 4√ 3 .5 = 20√ 3 ( cm^3 ).

Bài 1: Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm²

Lời giải:

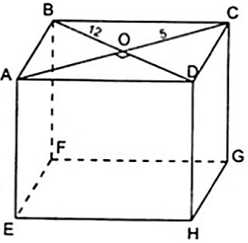
Áp dụng công thức: S_tp = S_xq + 2S_d

Hay S_xq = S_tp – 2S_d = 1280 – 2.1/2.1024

= 1280 – 240 = 1040( cm² )

Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)

Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:

BC² = BO² + OC² ⇒ BC² = 12² + 5² = 13² ⇔ BC = 13( cm )

Chu vi đáy là 2p = 4.13 = 52( cm )

Áp dụng công thức S_xq = 2p.h

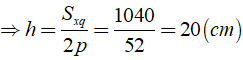
Bài 2: Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm³ ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?

Lời giải:

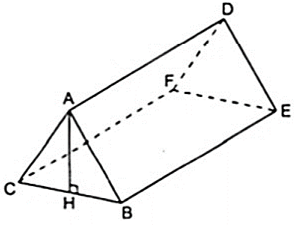
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h

Ta có: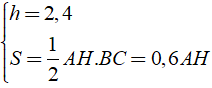

Do đó: V = S.h = 0,6AH.2,4 = 1,44AH

Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

---