Lý thuyết Hình thang lớp 8 (hay, chi tiết)

Bài viết Lý thuyết Hình thang lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Hình thang.

Lý thuyết Hình thang lớp 8 (hay, chi tiết)

Bài giảng: Bài 2: Hình thang – Cô Phạm Thị Huệ Chi (Giáo viên Meraki Center)

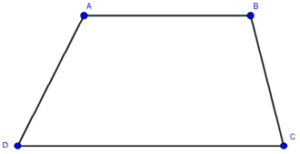
1. Định nghĩa

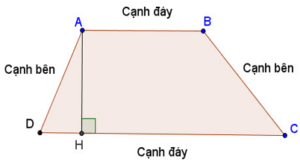
Hình thang là tứ giác có hai cạnh đối song song.

   Hai cạnh song song gọi là hai đáy.

   Hai cạnh còn lại gọi là hai cạnh bên.

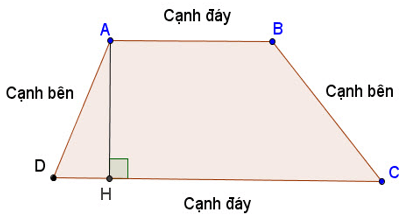
Gọi AH là đường vuông góc kẻ từ A đến đường thẳng CD, đoạn thẳng AH được gọi là đường cao của hình thang

Nhận xét:

   Nếu một hình thang có hai cạnh bên song song thì hai canh bên bằng nhau, hai cạnh đáy bằng nhau.

   Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.

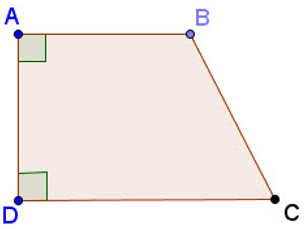
2. Hình thang vuông

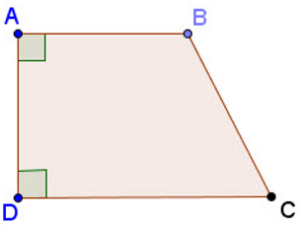
Định nghĩa: Hình thang vuông là hình thang có một góc vuông

Dấu hiệu nhận biết: Hình thang có một góc vuông là hình thang vuông

Ví dụ: Cho hình thang ABCD ( AB//CD ) có Aˆ – Dˆ = 30⁰,Bˆ = 2Cˆ. Tính các góc của hình thang

Lời giải:

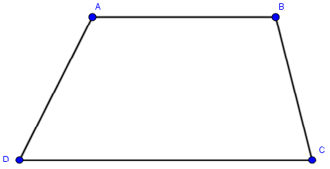
Trong hình thang ABCD có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.       ( 1 )

Theo giả thiết, ta có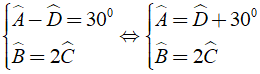
      ( 2 )

Ta lại có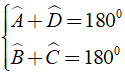
      ( 3 ) (do góc Dˆ bằng góc ngoài của góc Aˆ, góc Cˆ bằng góc ngoài của góc Bˆ )

Từ ( 2 ),( 3 ) ta có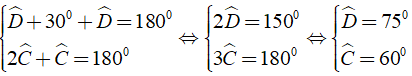

Khi đó Aˆ = Dˆ + 30^o = 75^o + 30^o = 105^o; Bˆ = 2Cˆ = 120⁰.

Bài 1: Hình thang vuông ABCD có Aˆ = Dˆ = 90⁰; AB = AD = 3cm;CD = 6cm. Tính số đo góc B và C của hình thang ?

Lời giải:

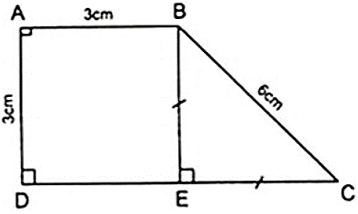
Kẻ BE ⊥ CD thì AD//BE do cùng vuông góc với CD

+ Hình thang ABED có cặp cạnh bên song song là hình bình hành.

Áp dụng tính chất của hình bình hành ta có

AD = BE = 3cm

Xét Δ BEC vuông tại E có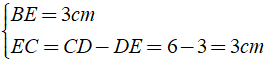

⇒ Δ BEC là tam giác vuông cân tại E.

Khi đó ta có: Cˆ = 45⁰ và ABCˆ = 90⁰ + 45⁰ = 135⁰.

Bài 2: Cho hình thang ABCD( AB//CD ), hai đường phân giác của góc C và D cắt nhau tại I thuộc đáy AB. Chứng minh rằng tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang

Lời giải:

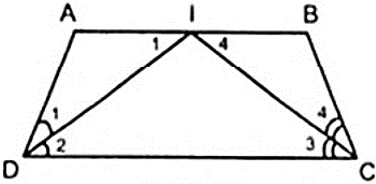
Áp dụng tính chất so le của AB//CD và giả thiết ta có:

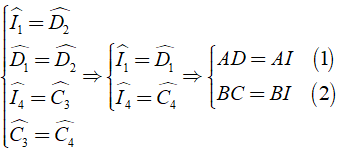
(vì trong một tam giác đối diện với hai góc bằng nhau là hai cạnh bằng nhau)

Cộng vế theo vế của ( 1 ) và ( 2 ) ta được: AD + BC = AB

Điều đó chứng tỏ tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang

Bài giảng: Bài 2: Hình thang – Cô Vương Thị Hạnh (Giáo viên Meraki Center)

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

---