Lý thuyết Hình Trụ – Diện tích xung quanh và thể tích của hình trụ lớp 9 (hay, chi tiết)

Bài viết Lý thuyết Hình Trụ – Diện tích xung quanh và thể tích của hình trụ lớp 9 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Hình Trụ – Diện tích xung quanh và thể tích của hình trụ.

Lý thuyết Hình Trụ – Diện tích xung quanh và thể tích của hình trụ lớp 9 (hay, chi tiết)

1. Hình trụ

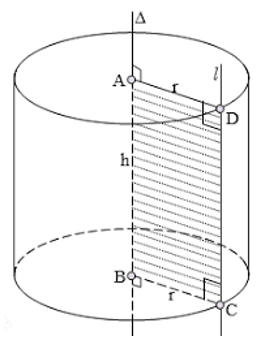
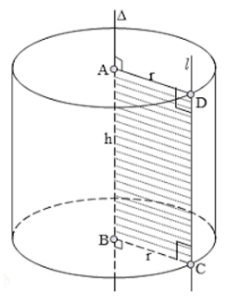
Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.

    + Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.

    + Đường thẳng AB được gọi là trục của hình trụ.

    + Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.

2. Cắt hình trụ bởi một mặt phẳng

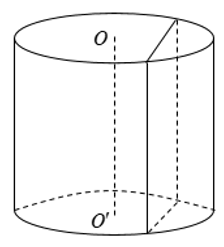
    + Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.

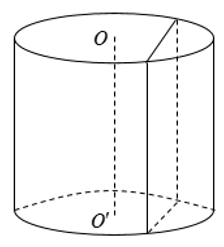
    + Khi cắt hình trụ bởi một mặt phẳng song song với trục OO’ thì mặt cắt là một hình chữ nhật

3. Diện tích và thể tích hình trụ

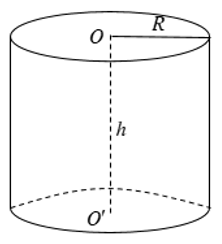
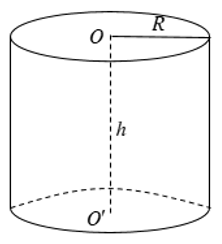
Cho hình trụ có bán kính đáy R và chiều cao h.

    + Diện tích xung quanh: S_xq = 2πRh

    + Diện tích toàn phần: S_tp = 2πRh + 2πR²

    + Thể tích: V = πR²h

4. Ví dụ cụ thể

Câu 1: Một hình trụ có bán kính đáy bằng 1/4 đường cao. Khi cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt là một hình chữ nhật có diện tích là 50cm². Tính diện tích xung quanh và thể tích hình trụ.

Lời giải:

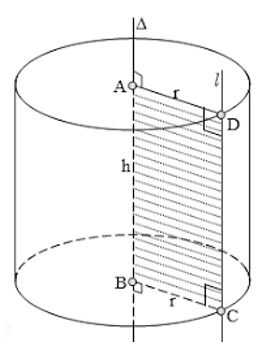
Theo giả thiết ta có

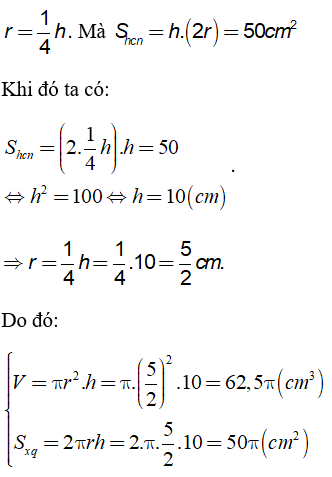
Câu 1: Tính diện tích xung quanh và diện tích toàn phần của hình sau

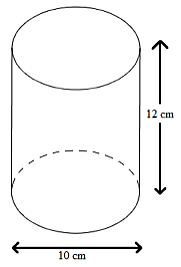
Lời giải:

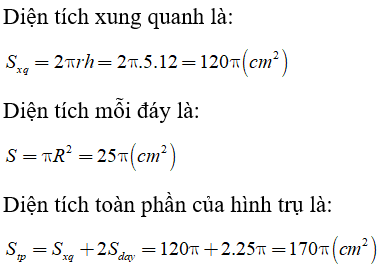
Câu 2: Hình chữ nhật ABCD có AB = a, BC = 3a . Quay hình chữ nhật quanh cạnh AB thì được thể tích V₁, quay quanh cạnh BC thì được thể tích V₂. Tỉ số thể tích giữa V₁ và V₂ là?

Lời giải:

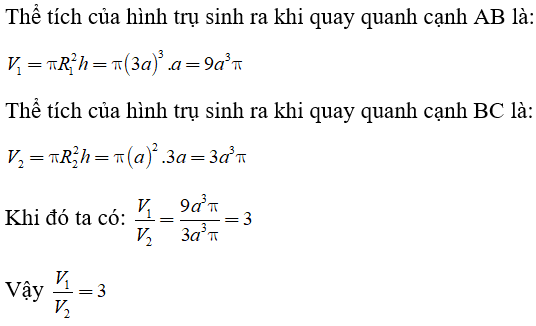
Xem thêm lý thuyết và các dạng bài tập Toán lớp 9 có lời giải hay khác: