Lý thuyết Nghiệm của đa thức một biến lớp 7 (hay, chi tiết)

Bài viết Lý thuyết Nghiệm của đa thức một biến lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Nghiệm của đa thức một biến.

Lý thuyết Nghiệm của đa thức một biến lớp 7 (hay, chi tiết)

1. Nghiệm của đa thức một biến

Nếu tại x = a, đa thức P(x) có giá trị bằng 0 thì ta nói a (hoặc x = a) là một nghiệm của đa thức đó.

Ví dụ 1: Kiểm tra xem mỗi số 1; 2; -1 có phải là một nghiệm của đa thức f(x) = x² – 3x + 2 hay không?

Hướng dẫn giải:

Ví dụ 2: Cho đa thức f(x) = x³ + 2x² + ax + 1

Tìm a biết rằng đa thức f(x) có một nghiệm x = -2

Hướng dẫn giải:

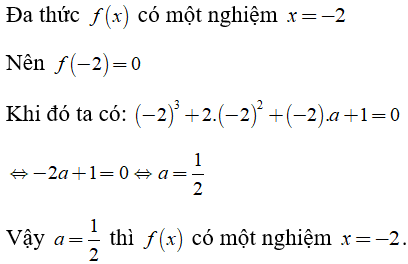
2. Chú ý:

   + Một đa thức (khác đa thức không) có thể có một nghiệm, hai nghiệm,… hoặc không có nghiệm.

   + Số nghiệm của một đa thức (khác đa thức không) không vượt quá bậc của nó. Chẳng hạn: đa thức bậc nhất chỉ có một nghiệm, đa thức bậc hai không quá hai nghiệm,…

Ví dụ: Tìm nghiệm của đa thức P(x) = 2y + 6

Từ 2y + 6 = 0 ⇒ 2y = -6 ⇒ y = -6/2 = -3

Vậy nghiệm của đa thức P(x) là -3.

Ví dụ 2: Giả sử a, b, c là các hằng số sao cho a + b + c = 0. Chứng minh rằng đa thức f(x) = ax² + bx + c có một nghiệm là x = 1 . Áp dụng để tìm một nghiệm của đa thức f(x) = 8x² – 6x – 2.

Hướng dẫn giải:

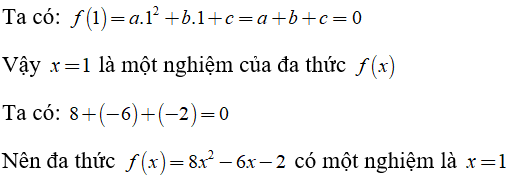
Bài 1: Chứng tỏ các đa thức sau không có nghiệm

a) P(x) = x² + 1                             b) Q(y) = 2y⁴ + 5

Lời giải:

a) Vì x² ≥ 0 nên x² + 1 ≥ 1

Do đó: P(x) = x² + 1 > 0 nên đa thức P(x) vô nghiệm.

b) Vì y⁴ ≥ 0 nên 2y⁴ + 5 > 0

Do đó: Q(y) = 2y⁴ + 5 > 0 nên đa thức Q(x) vô nghiệm.

Bài 2: Tìm nghiệm của đa thức

a) x² – 2003x – 2004 = 0

b) 2005x² – 2004x – 1 = 0

Lời giải:

a) Đa thức x² – 2003x – 2004 = 0 có hệ số a = 1, b = -2003, c = -2004

Khi đó ta có: a – b + c = 1 – (-2003) + (-2004) = 0

Nên đa thức x² – 2003x – 2004 = 0 có nghiệm x = -1

b) Đa thức 2005x² – 2004x – 1 = 0 có hệ số a = 2005, b = -2004, c = -1

Khi đó ta có: a + b + c = 2005 – 2004 – 1 = 0

Nên đa thức 2005x² – 2004x – 1 = 0 có nghiệm x = 1.

Bài 1: Cho đa thức f(x) = x² – x – 6

a) Tính giá trị của f(x) tại x = 1, x = 2, x = 3, x = –1, x = –2, x = –3.

b) Trong các giá trị trên, giá trị nào của x là nghiệm của đa thức f(x)?

Hướng dẫn giải:

a) • f(1) = 1² – 1 – 6 = –6

• f(2) = 2² – 2 – 6 = –4

• f(3) = 3² – 3 – 6 = 0

• f(–1) = (–1)² – (–1) – 6 = –4

• f(–2) = (–2)² – (–2) – 6 = 0

• f(–3) = (–3)² – (–3) – 6 = 6

b) Giá trị x = 3 và x = –2 là nghiệm của đa thức f(x).

Bài 2: Tìm nghiệm của các đa thức sau:

a) (x – 3)(x + 3);

b) (x – 2)(x² + 2);

c) 6 – 2x;

d) (x³ – 8)(x – 3).

Hướng dẫn giải:

a) (x – 3)(x + 3)

x – 3 = 0 hoặc x + 3 = 0

x = 3 hoặc x = –3

Vậy x = 3 và x = –3 là các nghiệm của đa thức (x – 3)(x + 3).

b) (x – 2)(x² + 2)

x – 2 = 0 hoặc x² + 2 = 0

• Với x – 2 = 0 thì x = 2

• Với x² + 2 = 0, nhận thấy x² > 0 với mọi x nên  x² + 2 > 0 với mọi x.

Do đó, không có giá trị nào của x để x² + 2 = 0

Vậy x = 2 là nghiệm của đa thức (x – 2)(x² + 2).

c) Xét 6 – 2x = 0 nên x = 3

Vậy x = 3 là nghiệm của đa thức 6 – 2x.

d) (x³ – 8)(x – 3) = 0

x³ – 8 = 0 hoặc x – 3 = 0

x³ = 8 hoặc x – 3 = 0

x = 2 hoặc x – 3 = 0

Vậy x = 3 và x = 2 là các nghiệm của đa thức (x³ – 8)(x – 3).

Bài 3: Chứng tỏ các đa thức sau không có nghiệm:

a) 10x² + 3

b) x² + 1.

Hướng dẫn giải:

a) Vì x² luôn dương với mọi x nên 10x² + 3 > 0 với mọi x.

Vậy không tồn tại x để đa thức bằng 0 hay đa thức không có nghiệm.

b) Vì x² luôn dương với mọi x nên x² + 1 > 0 với mọi x.

Vậy không tồn tại x để đa thức bằng 0 hay đa thức không có nghiệm.

Bài 4: Xác định hệ số tự do c để đa thức f(x) = 4x² – 7x + c có nghiệm bằng 5.

Hướng dẫn giải:

Để đa thức f(x) = 4x² − 7x + c có nghiệm bằng 5.

Khi đó f(5) = 0 nên 4.5² – 7.5 + c = 0.

Do đó c = –65.

Vậy với c = –6 thì đa thức có nghiệm bằng 5.

Bài 5: Lập đa thức một biến trong mỗi trường hợp sau:

a) Chỉ có một nghiệm là −25;

b) Vô nghiệm.

Hướng dẫn giải:

a) Đa thức chỉ có một nghiệm là −25.

Do đó A = 5x + 2.

b) Đa thức một biến vô nghiệm có thể là D = x² + 1.

Bài 6: Chứng minh rằng đa thức P: x = x³ + 2x² – 3x + 1 có duy nhất một nghiệm nguyên.

Bài 7. Tìm nghiệm các đa thức sau:

a) 3x + 6;

b) 2x² – 32;

c) 2x + 7 – (x + 14);

d) x² – 6x.

Bài 8. Cho đa thức f(x) = x⁴ + 2x³ – 2x² – 6x + 5. Trong các số sau: 1; −1; 2; −2 số nào là nghiệm của đa thức f(x).

Bài 9. Tìm nghiệm của đa thức:

a) M(x) = (6 – 3x)(−2x + 5);

b) N(x) = x² + x;

c) A(x) = 3x – 3.

Bài 10. Cho f(x) = 9 – x⁵ + 4x – 2x³ + x² – 7x⁴; g(x) = x⁵ – 9 + 2x² + 7x⁴ + 2x³ – 3x.

a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến;

b) Tìm tổng h(x) = f(x) + g(x);

c) Tìm nghiệm của đa thức h(x).

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:

Lời giải bài tập lớp 7 sách mới:

---