Lý thuyết Phân tích đa thức thành nhân tử lớp 8 (hay, chi tiết) – Tổng hợp Lý thuyết Toán 8 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 8.-Lý thuyết Phân tích đa thức thành nhân tử lớp 8 (hay, chi tiết)
Lý thuyết Phân tích đa thức thành nhân tử lớp 8 (hay, chi tiết)
Bài viết Lý thuyết Phân tích đa thức thành nhân tử lớp 8 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Phân tích đa thức thành nhân tử.
Lý thuyết Phân tích đa thức thành nhân tử lớp 8 (hay, chi tiết)
Bài giảng: Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung – Cô Phạm Thị Huệ Chi (Giáo viên Meraki Center)
1.Khái niệm về phương pháp đặt nhân tử chung
Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.
Ứng dụng: Việc phân tích đa thức thành nhân tử giúp ta có thể thu gọc biểu thức, tính nhanh và giải phương trình dễ dàng.
2.Phương pháp đặt nhân tử chung
+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.
Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.
( lưu ý tính chất: A = -(-A)).
3.Ví dụ áp dụng
Ví dụ: Phân tích đa thức sau thành nhân tử
a, 4x2 – 6x
b, 9x4y3 + 3x2y4
Lời giải:
a)Ta có : 4x2 – 6x = 2x.2x – 3.2x = 2x( 2x – 3 ).
b)Ta có: 9x4y3 + 3x2y4 = 3x2y3.3x2 + 3x2y3y = 3x2y3(3x2 + 1)
1.Phương pháp dùng hằng đẳng thức
+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.
+ Cần chú ý đến việc vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.
2.Ví dụ áp dụng
Ví dụ: Phân tích đa thức sau thành nhân tử
a, 9x2 – 1
b, x2 + 6x + 9.
Lời giải:
a)Ta có: 9x2 – 1 = ( 3x )2 – 12 = ( 3x – 1 )( 3x + 1 )
(áp dụng hằng đẳng thức A2 – B2 = ( A – B )( A + B ) )
b)Ta có: x2 + 6x + 9 = x2 + 2.x.3 + 32 = ( x + 3 )2.
(áp dụng hằng đẳng thức ( A + B )2 = A2 + 2AB + B2 )
1.Phương pháp nhóm hạng tử
+ Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.
+ Ta nhận xét để tìm cách nhóm hạng tử một cách thích hợp (có thể giao hoán và kết hợp các hạng tử để nhóm) sao cho sau khi nhóm, từng nhóm đa thức có thế phân tích được thành nhân tử bằng phương pháp đặt nhân tử chung, bằng phương pháp dùng hằng đẳng thức. Khi đó đa thức mới phải xuất hiện nhân tử chung.
+ Ta áp dụng phương pháp đặt thành nhân tử chung để phân tích đa thức đã cho thành nhân tử.
2.Chú ý
+ Với một đa thức, có thể có nhiều cách nhóm các hạng tử một cách thích hợp.
+ Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).
+ Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.
+ Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.
3.Ví dụ áp dụng
Ví dụ: Phân tích các đa thức sau thành nhân tử.
a, x2 – 2xy + xy2 – 2y3.
b, x2 + 4x – y2 + 4.
Lời giải:
a)Ta có x2 – 2xy + xy2 – 2y3 = ( x2 – 2xy ) + ( xy2 – 2y3 ) = x( x – 2y ) + y2( x – 2y )
= ( x + y2 )( x – 2y )
b)Ta có x2 + 4x – y2 + 4 = ( x2 + 4x + 4 ) – y2 = ( x + 2 )2 – y2 = ( x + 2 – y )( x + y + 2 )
1.Phương pháp thực hiện
Ta tìm hướng giải bằng cách đọc kỹ đề bài và rút ra nhận xét để vận dụng các phương pháp đã biết:
+ Đặt nhân tử chung
+ Dùng hằng đẳng thức
+ Nhóm nhiều hạng tử và phối hợp chúng
⇒ Để phân tích đa thức thành nhân tử.
2.Chú ý
Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.
3.Ví dụ áp dụng
Ví dụ: Phân tích đa thức thành nhân tử
x2 + 4x – 2xy – 4y + y2.
2xy – x2 – y2 + 16.
Lời giải:
a)Ta có x2 + 4x – 2xy – 4y + y2 = ( x2 – 2xy + y2 ) + ( 4x – 4y ) = ( x – y )2 + 4( x – y )
= ( x – y )( x – y + 4 ).
b)Ta có: 2xy – x2 – y2 + 16 = 16 – ( x2 – 2xy + y2 ) = 16 – ( x – y )2
= ( 4 – x + y )( 4 + x – y ).
Bài 1: Phân tích các đa thức sau thành nhân tử
a, ( ab – 1 )2 + ( a + b )2
b, x3 + 2x2 + 2x + 1
c, x2 – 2x – 4y2 – 4y
Lời giải:
a)Ta có ( ab – 1 )2 + ( a + b )2 = a2b2 – 2ab + 1 + a2 + 2ab + b2
= a2b2 + a2 + b2 + 1 = ( a2b2 + a2 ) + ( b2 + 1 )
= a2( b2 + 1 ) + ( b2 + 1 ) = ( a2 + 1 )( b2 + 1 )
b)Ta có x3 + 2x2 + 2x + 1 = ( x3 + 1 ) + ( 2x2 + 2x )
= ( x + 1 )( x2 – x + 1 ) + 2x( x + 1 ) = ( x + 1 )( x2 + x + 1 )
c)Ta có x2 – 2x – 4y2 – 4y = ( x2 – 4y2 ) – ( 2x + 4y )
= ( x – 2y )( x + 2y ) – 2( x + 2y )
= ( x + 2y )( x – 2y – 2 ).
Bài 2: Tính giá trị của biểu thức sau A = x6 – 2x4 + x3 + x2 – x, biết x3 – x = 6.
Lời giải:
Ta có: A = x6 – 2x4 + x3 + x2 – x = ( x6 – 2x4 + x2 ) + ( x3 – x )
= ( x3 – x )2 + ( x3 – x )
Với x3 – x = 6 = ( x3 – x )2 + ( x3 – x ), ta có A = 62 + 6 = 36 + 6 = 42.
Vậy A = 42.
Bài 3: Tìm x biết
Lời giải:
Bài 4. Phân tích các đa thức sau thành nhân tử:
a) A = x4 – 11x3 + 26x2 – 22x + 48;
b) B = x5 + 3x4 + x3 − 11x2 − 30x – 20.
Lời giải:
a) A = x4 – 8x3 – 3x3 + 24x2 + 2x2 – 16x – 6x + 48
= (x – 8)(x3 – 3x2 + 2x – 6)
= (x – 8)(x – 3)(x2 + 2).
b) B = x5 + 3x4 + x3 − 11x2 − 30x – 20
= x5 – 5x3 + 3x4 – 15x2 + 6x3 – 30x + 4x2 – 20
= (x2 − 5)(x3 + 3x2 + 6x + 4)
= (x2 − 5)(x3 + 2x2 + 4x + x2 + 2x + 4)
= (x2 − 5)(x2 + 2x + 4) (x + 1).
Bài 5. Phân tích các đa thức sau thành nhân tử.
a) A = x4 + 5x3 + 7x2 + 5x + 6
b) B = x3 − 11x2 + 10x
Lời giải:
a) A = x4 + 5x3 + 7x2 + 5x + 6
= x4 + 3x3 + 2x3 + 6x2 + x2 + 3x + 2x + 6
= (x + 3)(x3 + 2x2 + x + 2)
= (x + 3)(x3 + x + 2x2 + 2)
= (x + 3)(x2 + 1)(x + 2).
b) B = x3 − 11x2 + 10x
= x(x2 − 11x+ 10)
= x(x2 – x – 10x + 10)
= x(x – 1)(x – 10).
Bài 6. Tìm x, biết:
a) x3 − 5x2 − 9x + 10 = –35
b) x5 − 4x3 + 5x2 – 20 = 0
Lời giải:
a) x3 − 5x2 − 9x + 10 = –35
x3 − 5x2 − 9x + 45 = 0
x(x2 – 9) – 5(x2 – 9) = 0
(x – 5)(x2 – 9) = 0
(x – 5)(x – 3)(x + 3) = 0
x – 5 = 0 hoặc x – 3 = 0 hoặc x + 3 = 0
x = 5 hoặc x = 3 hoặc x = –3
Vậy x ∈ {–3; 3; 5}.
b) x5 − 4x3 + 5x2 – 20 = 0
x3(x2 – 4) + 5(x2 – 4) = 0
(x2 – 4)(x3 + 5) = 0
(x + 2)(x – 2)(x3 + 5) = 0
x + 2 = 0 hoặc x – 2 = 0 hoặc x3 + 5 = 0
x = 2 hoặc x = – 2 hoặc x = −53.
Vậy x∈−2; −53 ; 2 .
Bài 7. Cho P = x2 + 11x + 24. Tìm x để P chia hết cho 4.
Lời giải:
P = x2 + 11x + 24
= x2 + 3x + 8x + 24
= (x + 3)(x + 8)
Nhận thấy, (x + 3) và (x + 8) không cùng lúc chẵn.
Nên P ⁝ 4 khi và chỉ khi (x + 3) ⁝ 4 hoặc (x + 8) ⁝ 4.
• Trường hợp 1: x + 3 ⁝ 4 nên x = 4k + 1 (k ∈ ℤ).
• Trường hợp 2: x + 8 ⁝ 4 nên x = 4h (h ∈ ℤ).
Bài 8. Tìm x, biết: x4 + 10x3 + 35x2 + 50x + 24 = 0.
Lời giải:
x4 + 10x3 + 35x2 + 50x + 24 = 0
x4 + x3 + 9x3 + 9x2 + 26x2 + 26x + 24x + 24 = 0
(x + 1)(x3 + 9x2 + 26x + 24) = 0
(x + 1)( x3 + 2x2 + 7x2 + 14x + 12x + 24) = 0
(x + 1)(x + 2)(x2 + 7x + 12) = 0
(x + 1)(x + 2)(x2 + 3x + 4x + 12) = 0
(x + 1)(x + 2)(x + 3)(x + 4) = 0
Vậy x ∈ {–1; –2; –3; –4}.
Bài 9. Tìm nhân tử chung của các biểu thức:
a) A = 5×3+16×2+8x+16+3x;
b) B = 5×4+21×2+19+3×2.
Bài 10. Cho biểu thức P = x4 + x3 + 2x + 2. Với giá trị nào của x thì P ⁝ 10?
Bài 11. Cho biểu thức P = x4 + 8x3 + 32x2 + 256x. Với giá trị nào của x thì P ⁝ 16?
Bài 12. Tìm x, biết: x2+2x+5+7x−2=0.
Bài 13. Tìm nhân tử chung của biểu thức: P = 2x4 − 11x3 − 7x2 + 51x + 45.
Bài giảng: Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Bài giảng: Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Bài giảng: Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Bài giảng: Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp – Cô Vương Thị Hạnh (Giáo viên Meraki Center)
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

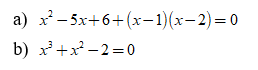

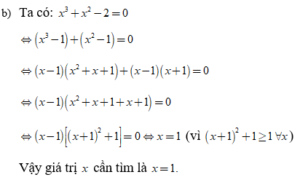

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: [email protected]