Lý thuyết Phép vị tự lớp 11 (hay, chi tiết)

Bài viết Lý thuyết Phép vị tự lớp 11 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Phép vị tự.

Lý thuyết Phép vị tự

Bài giảng: Bài 7: Phép vị tự – Thầy Lê Thành Đạt (Giáo viên Meraki Center)

1. Định nghĩa

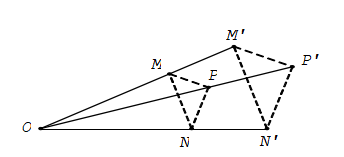
    Cho điểm O và số k ≠ 0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho OM’→ = kOM→ được gọi là phép vị tự tâm O tỉ số k.

    Phép vị tự tâm O tỉ số k thường được kí hiệu là V_(O;k).

Nhận xét

    Phép vị tự biến tâm vị tự thành chính nó.

    Khi k = 1, phép vị tự là đồng nhất.

    Khi k = –1, phép vị tự là phép đối xứng tâm.

    M’ = V_{(O; k)}(M) ⇔ M = V_{(O; 1/k)}(M’)

2. Tính chất

Tính chất 1

    Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì M’N’→ = kMN→ và M’N’ = |k|.MN.

Tính chất 2

Phép vị tự tỉ số k:

    Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy;

    Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng;

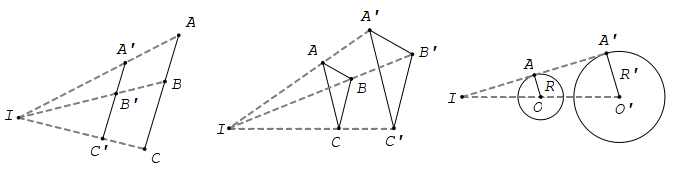
    Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó;

    Biến đường tròn bán kính R thành đường tròn bán kính |k|R.

Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác: