Lý thuyết Phương trình đường thẳng lớp 10 (hay, chi tiết)

---

---

Bài viết Lý thuyết Phương trình đường thẳng lớp 10 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Lý thuyết Phương trình đường thẳng.

Lý thuyết Phương trình đường thẳng

Bài giảng: Bài 1: Phương trình đường thẳng – Thầy Lê Thành Đạt (Giáo viên VietJack)

Vectơ 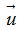được gọi là vectơ chỉ phương của đường thẳng ∆ nếu 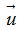≠ 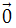và giá của song song hoặc trùng với ∆.

Nhận xét. Một đường thẳng có vô số vectơ chỉ phương.

Đường thẳng ∆ đi qua điểm M₀(x₀, y₀) và có VTCP 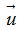= (a; b)

=> phương trình tham số của đường thẳng ∆ có dạng

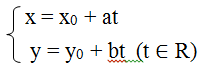
Nhận xét. Nếu đường thẳng ∆ có VTCP 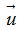= (a; b)

thì có hệ số góc k =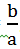

Vectơ 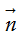được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu 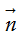≠ 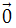và 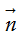vuông góc với vectơ chỉ phương của ∆.

Nhận xét.

+) Một đường thẳng có vô số vectơ pháp tuyến.

Đường thẳng ∆ đi qua điểm M₀(x₀, y₀) và có VTPT 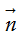= (A; B)

=> phương trình tổng quát của đường thẳng ∆ có dạng

A(x – x₀) + B(y – y₀) = 0 hay Ax + By + C = 0 với C = –Ax₀ – By₀.

Nhận xét.

+) Nếu đường thẳng ∆ có VTPT 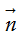= (A; B) thì có hệ số góc k =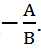

+) Nếu A, B, C đều khác 0 thì ta có thể đưa phương trình tổng quát về dạng

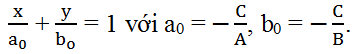
Phương trình này được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt Ox và Oy lần lượt tại M(a0; 0) và N(0; b0).

Xét hai đường thẳng có phương trình tổng quát là

∆₁: a₁x + b₁y + c₁ = 0 và ∆₂: a₂x + b₂y + c₂ = 0

Tọa độ giao điểm của ∆₁ và ∆₂ là nghiệm của hệ phương trình:

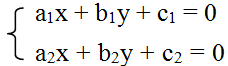
+) Nếu hệ có một nghiệm (x₀; y₀) thì ∆₁ cắt ∆₂ tại điểm M₀(x₀, y₀).

+) Nếu hệ có vô số nghiệm thì ∆₁ trùng với ∆₂.

+) Nếu hệ vô nghiệm thì ∆₁ và ∆₂ không có điểm chung, hay ∆₁ song song với ∆₂

Cách 2. Xét tỉ số

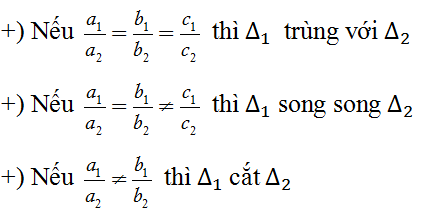
Cho hai đường thẳng

∆₁: a₁x + b₁y + c₁ = 0 có VTPT 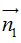= (a₁; b₁);

∆₂: a₂x + b₂y + c₂ = 0 có VTPT 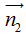= (a₂; b₂);

Gọi α là góc tạo bởi giữa hai đường thẳng ∆₁ và ∆₂

Khi đó

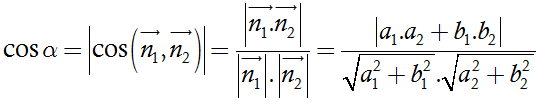
Khoảng cách từ M₀(x₀, y₀) đến đường thẳng ∆: ax + by + c = 0 được tính theo công thức

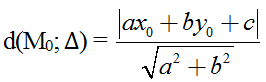
Nhận xét. Cho hai đường thẳng ∆₁: a₁x + b₁y + c₁ = 0 và ∆₂: a₂x + b₂y + c₂ = 0 cắt nhau thì phương trình hai đường phân giác của góc tạo bởi hai đường thẳng trên là:

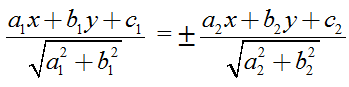
1. Phương trình đường tròn có tâm và bán kính cho trước

Trong mặt phẳng Oxy, đường tròn (C ) tâm I(a; b) bán kính R có phương trình:

(x – a)² + (y – b)² = R²

Chú ý. Phương trình đường tròn có tâm là gốc tọa độ O và bán kính R là x² + y² = R²

2. Nhận xét

+) Phương trình đường tròn (x – a)² + (y – b)² = R² có thể viết dưới dạng

x² + y² – 2ax – 2by + c = 0

trong đó c = a² + b² – R².

+) Phương trình x² + y² – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi a² + b² – c² > 0. Khi đó, đường tròn (C) có tâm I(a; b), bán kính R =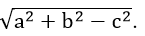

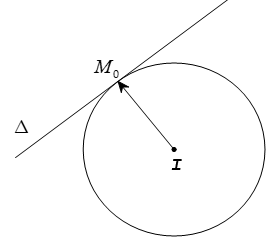
3. Phương trình tiếp tuyến của đường tròn

Cho đường tròn (C) có tâm I(a; b) và bán kính R.

Đường thẳng Δ là tiếp tuyến với (C) tại điểm M_o(x_o; y_o).

Ta có

+) M_o(x_o; y_o) thuộc Δ.

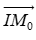+) = (x0 – a; y0 – b) là vectơ pháp tuyến của Δ.

Do đó Δ có phương trình là

(x_o – a).(x – x_o) + (y_o – b).(y – y_o) = 0.

1. Định nghĩa: Cho hai điểm cố định F₁ và F₂ với F₁F₂ = 2c (c > 0). Tập hợp các điểm M thỏa mãn MF1 + MF2 = 2a (a không đổi và a > c > 0) là một đường Elip.

+) F₁, F₂ là hai tiêu điểm.

+) F₁F₂ = 2c là tiêu cự của Elip

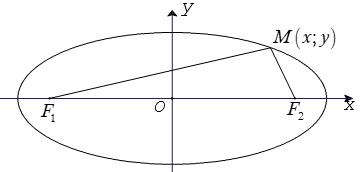
2. Phương trình chính tắc của Elip

(E): 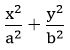= 1 với a² = b² + c²

Do đó điểm M(x_o; y_o) ∈ (E) <=> 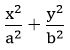= 1 và |x_o| ≤ a, |y_o| ≤ b.

3. Tính chất và hình dạng của Elip

+) Trục đối xứng Ox (chứa trục lớn), Oy (chứa trục bé).

+) Tâm đối xứng O.

+) Tọa độ các đỉnh A₁(–a; 0), A₂(a; 0), B₁(0; –b), B₂(0; b).

+) Độ dài trục lớn 2a. Độ dài trục bé 2b.

+) Tiêu điểm F₁(–c; 0), F₂(c; 0).

+) Tiêu cự 2c.

Xem thêm các dạng bài tập Toán 10 có đáp án hay khác:

Lời giải bài tập lớp 10 sách mới:

---

---

---