Lý thuyết Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn lớp 7 (hay, chi tiết) – Tổng hợp lý thuyết Toán lớp 7 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 7.-Lý thuyết Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn lớp 7 (hay, chi tiết)
Lý thuyết Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn lớp 7 (hay, chi tiết)
Bài viết Lý thuyết Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn.
Lý thuyết Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn lớp 7 (hay, chi tiết)
Bài giảng: Bài 9: Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn – Cô Vũ Xoan (Giáo viên Meraki Center)
1. Số thập phân hữu hạn
Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.
Ví dụ:
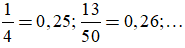
+ Phân số -6/75 viết được dưới dạng số thập phân hữu hạn vì:
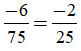
mẫu số 25 = 52 không có ước nguyên tố khác 2 và 5.
Ta có:
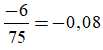
2. Số thập phân vô hạn tuần hoàn
Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.
Ví dụ:
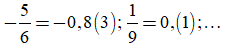
+ Phân số 7/30 được viết dưới dạng số thập phân vô hạn tuần hoàn vì mẫu 30 = 2.3.5 có ước nguyên tố là 3 khác 2 và 5.
3. Chú ý
Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn tuần hoàn hoặc vô hạn tuần hoàn. Ngược lại, mỗi số thập phân hữu hạn tuần hoàn và vô hạn tuần hoàn biểu diễn một số hữu tỉ.
Ví dụ 1: Viết các số hữu tỉ dưới dạng phân số: 0,00(24); 0,75; 1,28; 0,(12); 1,3(4)
Hướng dẫn giải:
Ta có:
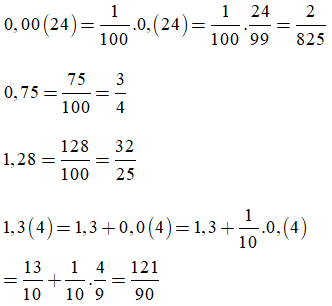
Ví dụ 2: Tìm x biết: 0,(12) : 1,(6) = x : 0,(3)
Hướng dẫn giải:
Ta có:
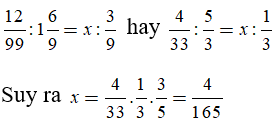
Bài 1: Viết các số hữu tỉ sau dưới dạng số tập phân hữu hạn hoặc vô hạn tuần hoàn:
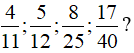
Lời giải:
Ta có:
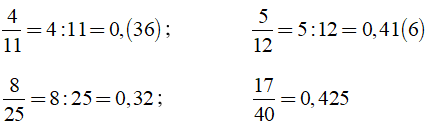
Bài 2: Tính [12,(1) – 2,3(6)] : 4(21)
Lời giải:
Ta có:
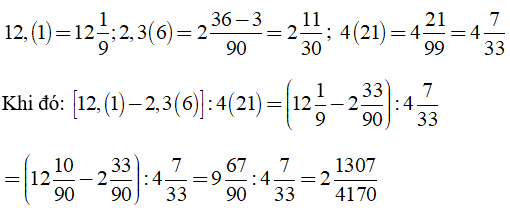
Bài 1. Thực hiện phép tính:
a) 723.[(-86)-4518];
b) 1627:(-35)+2827:35.
Hướng dẫn giải:
a) 723.[(-86)-4518];
=723[(-2418)-4518]
= 723.-24-4518=723.-6918
= 723.-3.233.6=-76.
b) 1627:(-35)+2827:35.
= 1627.-53+2827.53
= 53(-1627+2827)
= 53(-16-27+28+27)
= 53.12=20
Bài 2. Tính nhanh giá trị các biểu thức sau:
a) 2314.75-1314:57;
b) (-25+14:-7101).(5517-47.23).(1-513:513)
Hướng dẫn giải:
a) 2314.75-1314:57;
= 2314.75-1314.75
= 75(2314-1314)
= 75(23+14-13-14)
= 75.10=14
b) (-25+14:-7101).(5517-47.23).(1-513:513)
= (-25+14:-7101).(5517-47.23).(1-1)
= (-25+14:-7101).(5517-47.23).0=0
Bài 3. Viết các số hữu tỉ sau dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn:
2311; 415; 1625; 1733.
Hướng dẫn giải:
• 2311=23:11=2,(09);
• 415=4:15=0,2(6);
• 1625=16:25=0,64;
• 1733=17:33=0,(51).
Bài 4. Thực hiện phép tính được kết quả là
A. 584;
B. 845;
C. -584;
D. -845.
Hướng dẫn giải:
Đáp án đúng là: A
Ta có: (34+23):74-34
= (912+812).47-34
= 1712.47-34
= 1721-34
= 68-6384=584
Bài 5. Kết quả của phép tính 32-56:14+2 là
A. Là số tự nhiên;
B. Là số nguyên;
C. Là số hữu tỉ âm;
D. Là số hữu tỉ dương.
Hướng dẫn giải:
Đáp án đúng là D.
Ta có:
32-56:14+2
= 32-56.4+2
= 32-5.2.22.3+2
= 32-103+2
= 96-206+126
= 16>0.
Suy ra kết quả của phép tính là số hữu tỉ dương.
Bài 6. Viết các sô hữu tỉ sau dưới dạng phân số: 0,23; 0,(13); 0,125; 0,(51).
Bài 7. Tính: (-35+511):-37+(-25+611):(-37).
Bài 8. Tính giá trị của biếu thức: A=1-1+21-31-4.
Bài 9. Giá trị của biểu thức: B=34-35+37+311134-135+137+1311.
Bài 10. Cho A=45457575-171717191919. Chọn đáp án sai:
A. A < 1;
B. A là số hữu tỉ âm;
C. A là số hữu tỉ dương;
D. A là số hữu tỉ.
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:
Lời giải bài tập lớp 7 sách mới:

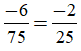
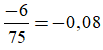

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn