Mặt phẳng tọa độ. Đồ thị của hàm số (Lý thuyết Toán lớp 8) | Cánh diều

Với tóm tắt lý thuyết Toán lớp 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số sách Cánh diều hay nhất, chi tiết
sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Mặt phẳng tọa độ. Đồ thị của hàm số (Lý thuyết Toán lớp 8) | Cánh diều

Lý thuyết Mặt phẳng tọa độ. Đồ thị của hàm số

1. Mặt phẳng tọa độ

Định nghĩa:

Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy.

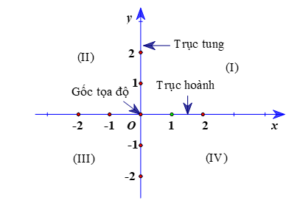
Trục Ox, Oy gọi là các trục tọa độ, Ox gọi là trục hoành, Oy gọi là trục tung. O gọi là gốc tọa độ.

Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.

Chú ý:

– Hai trục tọa độ chia mặt phẳng thành bốn góc: góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo thứ tự ngược chiều quay của kim đồng hồ.

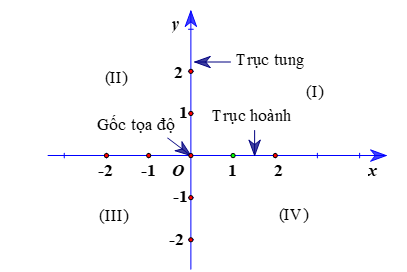
– Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau (nếu không có lưu ý gì thêm).

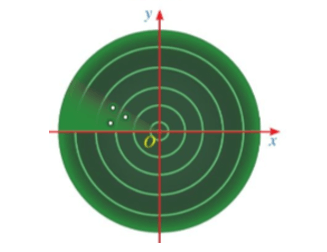
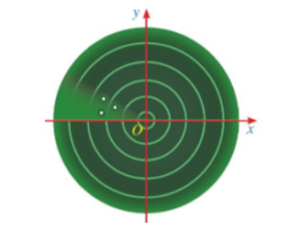
Ví dụ: Màn hình ra đa của đài kiểm soát không lưu gợi nên hình ảnh một mặt phẳng tọa độ và cả ba chấm sáng trên màn hình ra đa của đài kiểm soát không lưu đều nằm ở góc phần tư thứ II của mặt phẳng tọa độ.

2. Tọa độ của một điểm trong mặt phẳng tọa độ

Định nghĩa:

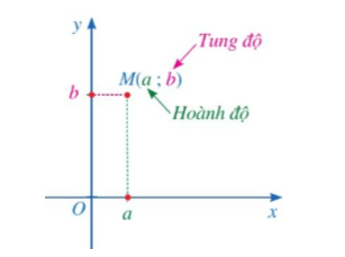
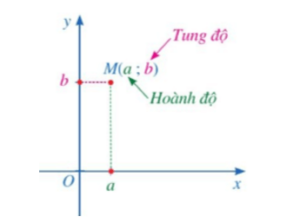
Cho điểm M trong mặt phẳng tọa độ Oxy. Giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy.

Cặp số (a; b) gọi là tọa độ của điểm M, a là hoành độ và b là tung độ của điểm M.

Điểm M có tọa độ (a; b) được kí hiệu là M(a; b).

Chú ý:

– Trong mặt phẳng tọa độ Oxy, mỗi điểm M xác định một cặp số (a; b). Ngược lại, mỗi cặp số (a; b) xác định một điểm M.

– Điểm nằm trên trục hoành có tung độ bằng 0.

– Điểm nằm trên trục tung có hoành độ bằng 0.

Ví dụ: Cho mặt phẳng tọa độ Oxy như hình vẽ.

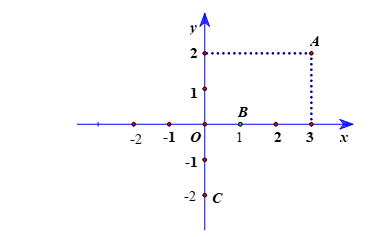
Khi đó:

– Điểm A(3; 2), hoành độ của điểm A là 3, tung độ của điểm A là 2.

– Điểm B(1; 0), hoành độ của điểm B là 1, tung độ của điểm B là 0.

– Điểm C(0; −2), hoành độ của điểm C là 0, tung độ của điểm C là −2.

3. Đồ thị của hàm số

Định nghĩa:

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ.

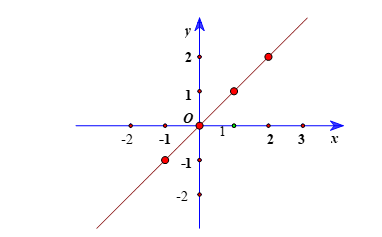
Ví dụ: Cho hàm số y = f(x) xác định bởi bảng 1 như sau:

Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm có tọa độ là các cặp số (−1;1), (0; 0), (1; 1), (2; 2). Tập hợp 4 điểm đó như hình bên dưới là đồ thị của hàm số đã cho ở bảng 1.

Bài tập Mặt phẳng tọa độ. Đồ thị của hàm số

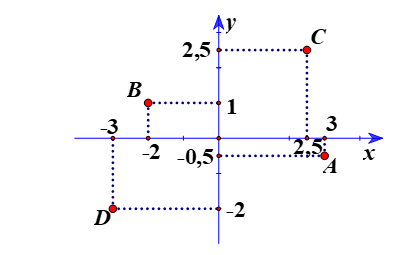
Bài 1: Vẽ mặt phẳng tọa độ Oxy và đánh dấu vị trí các điểm sau trên đó A(3; −0,5), B(−2; 1), C(2,5; 2,5), D(−3; −2).

Hướng dẫn giải

Cách xác định:

– Từ điểm biểu diễn hoành độ của điểm cho trước, kẻ một đường thẳng song song với trục tung.

– Tử điểm biểu diễn tung độ của điểm cho trước, kẻ một đường thẳng song song với trục hoành.

– Giao điểm của hai đường thẳng vừa dựng là điểm phải tìm.

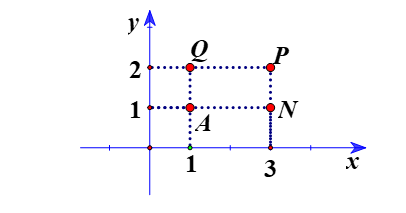
Bài 2: Viết tọa độ các điểm A, N, P, Q trong hình bên dưới.

Hướng dẫn giải

Cách xác định:

– Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.

– Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.

– Hoành độ và tung độ tìm được là tọa độ của điểm đã cho.

Từ đó, ta các định được tọa độ các điểm là: A(1; 1), N(3; 1), P(3; 2), Q(1; 2).

Học tốt Mặt phẳng tọa độ. Đồ thị của hàm số

Các bài học để học tốt Mặt phẳng tọa độ. Đồ thị của hàm số Toán lớp 8 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 8 Chân trời sáng tạo hay khác:

Xem thêm các tài liệu học tốt lớp 8 hay khác:

---