Nội dung bài viết
Tập hợp các số hữu tỉ (Lý thuyết Toán lớp 7) | Kết nối tri thức – Tóm tắt lý thuyết Toán lớp 7 Kết nối tri thức chi tiết đầy đủ Tập 1, Tập 2 giúp học sinh nắm vững kiến thức trọng tâm Toán 7.-Tập hợp các số hữu tỉ (Lý thuyết Toán lớp 7) – Kết nối tri thức
Tập hợp các số hữu tỉ (Lý thuyết Toán lớp 7) – Kết nối tri thức
Với tóm tắt lý thuyết Toán 7 Bài 1: Tập hợp các số hữu tỉ hay nhất, chi tiết sách Kết nối tri thức
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Tập hợp các số hữu tỉ (Lý thuyết Toán lớp 7) – Kết nối tri thức
Lý thuyết Tập hợp các số hữu tỉ
1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số
• Số hữu tỉ là số viết được dưới dạng phân số ab với a, b ∈ ℤ, b ≠ 0.
Tập hợp các số hữu tỉ được kí hiệu là ℚ .
• Cách biểu diễn số hữu tỉ ab trên trục số:
+ Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.
+ Điểm biểu diễn số hữu tỉ ab cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).
Ví dụ:
+ Các số – 7; 0,3; – 234 là các số hữu tỉ vì – 7 = −71 ; 0,3 = 310 ; – 234 = −114 .
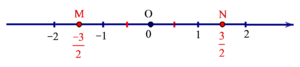
+ Biểu diễn số hữu tỉ 32 trên trục số ta làm như sau:
Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).
Số hữu tỉ 32 được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)
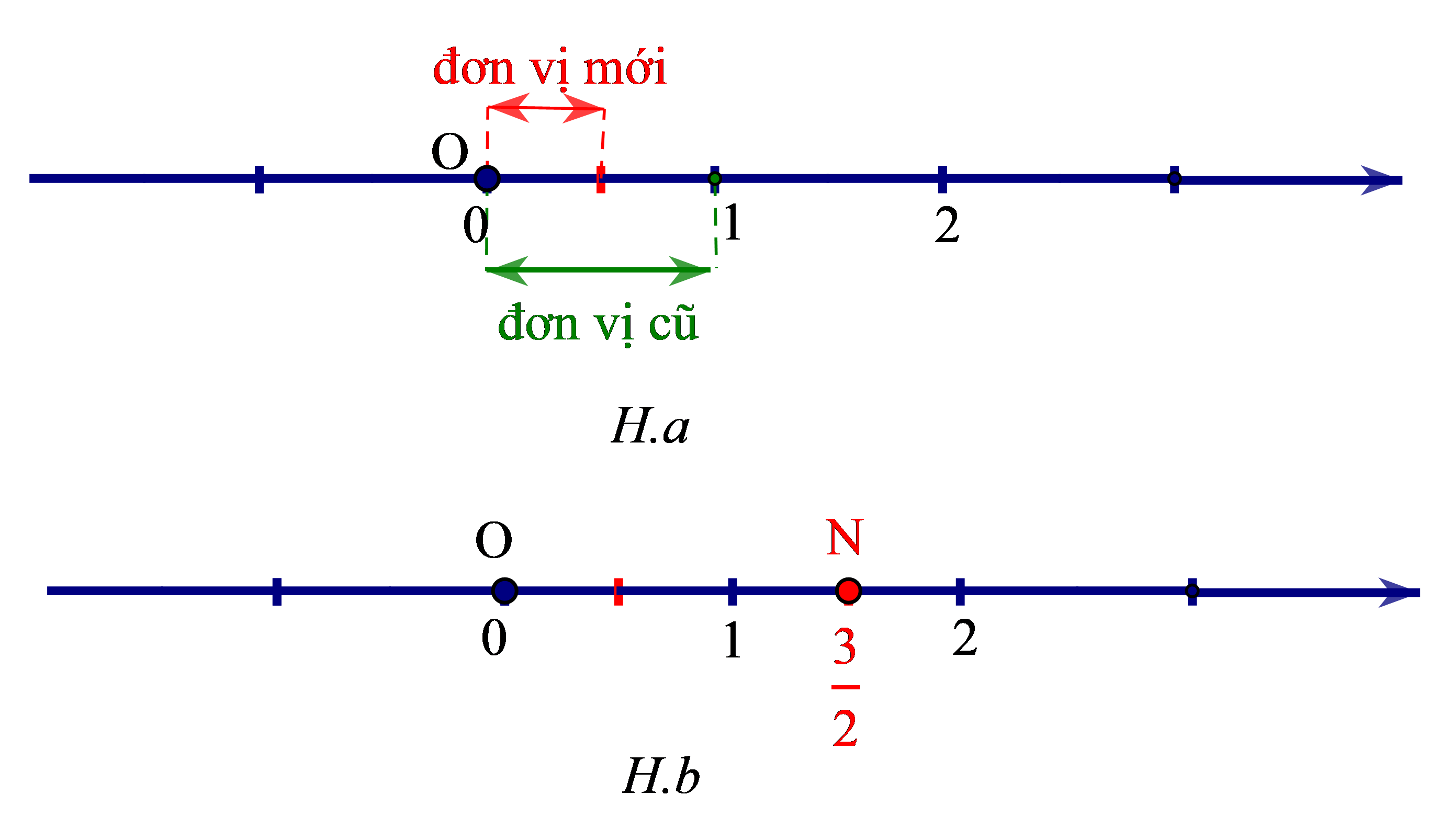
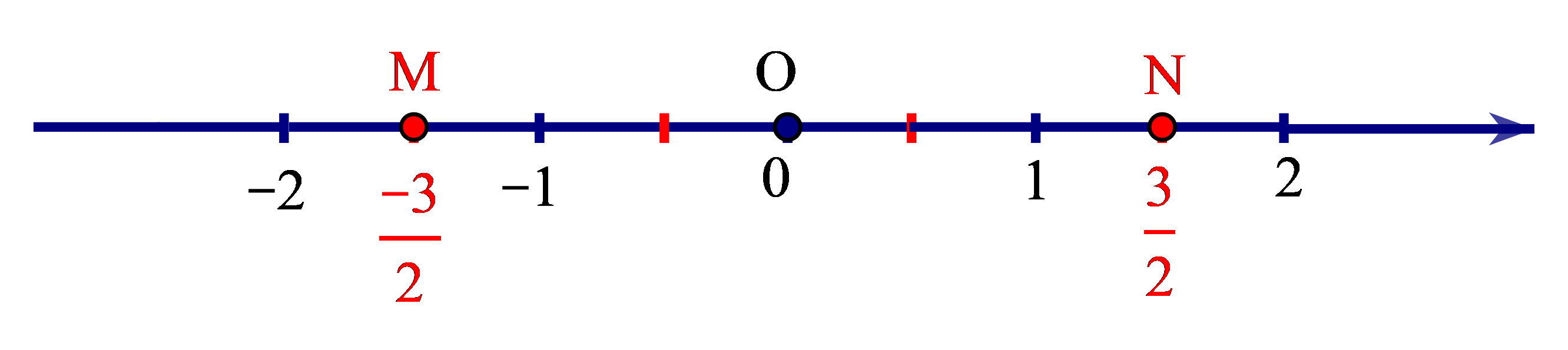
+ Số đối của số hữu tỉ 32là số hữu tỉ −32được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.
Chú ý:
• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.
• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.
• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.
2. Thứ tự trong tập hợp các số hữu tỉ
•Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.
•Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.
Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).
•Trên trục số, nếu a < b thì điểm a nằm trước điểm b.
Ví dụ:
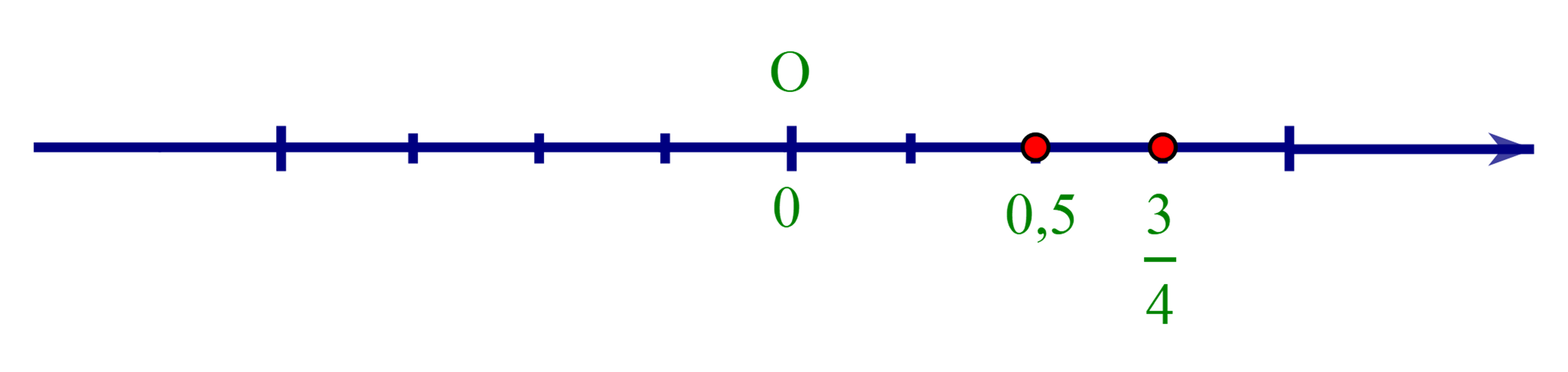
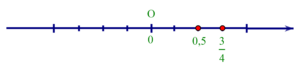
+ So sánh 0,5 và 34ta làm như sau: 0,5 = 510=24và 34. Vì 24< 34nên 0,5 < 34.
+ 0,5 < 34nên 0,5 nằm trước 34trên trục số.
+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ 56và 65như sau:
Vì 56< 1 và 1 < 65nên 56< 65.
Chú ý:
• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
Bài tập Tập hợp các số hữu tỉ
Bài 1. Điền kí hiệu (∈, ∉) thích hợp vào chỗ chấm:
a) 0,25 … ℚ ;
b) −57 … ℚ ;
c) 0 … ℚ ;
d) 318 … ℚ .
Hướng dẫn giải
a) Vì 0,25 = 14 nên 0,25 ∈ ℚ
b) −57 ∈ ℚ
c) Vì 0 = 01 nên 0 ∈ ℚ
d) Vì 318 = 258 nên 318 ∈ ℚ .
Bài 2. Cho trục số sau:

a) Các điểm A, B, C, D biểu diễn những số hữu tỉ nào?
b) Tìm số đối của các số hữu tỉ trên và biểu diễn chúng trên trục số.
Hướng dẫn giải
a) Ta thấy đoạn thẳng đơn vị cũ (ví dụ đoạn từ 0 đến 1) được chia thành 5 phần bằng nhau nên đoạn đơn vị mới bằng 15 đơn vị cũ. Do đó:
Điểm A nằm trước gốc O và cách gốc O một khoảng bằng 7 đơn vị nên nó biểu diễn số hữu tỉ −75 .
Tương tự, ta có được:
Điểm B biểu diễn số hữu tỉ −25 .
Điểm C biểu diễn số hữu tỉ 45 .
Điểm D biểu diễn số hữu tỉ 95 .
b) Số đối của −75 là −−75=75
Số đối của −25 là −−25=25
Số đối của 45 là −45
Số đối của 95 là −95
Biểu diễn trên trục số:

Bài 3. So sánh:
a) – 1,25 và – 1,125;
b) 0,8 và 815 ;
c) −219 và −1019 ;
d) 223 và 176 ;
e) 12022 và 12023 ;
f) – 5,6 và 12 ;
g) 79 và 1,5.
Hướng dẫn giải
a) Có 1,25 > 1,125 nên – 1,25 < – 1,125
b) Có 0,8 = 810=45=1215 , vì 1215 > 815 . Nên 0,8 > 815
c) Có 219 < 1019 nên −219 > −1019
d) Có 223=83=166 , vì 166 < 176 . Nên 223 < 176
e) 12022 > 12023
f) Có – 5,6 < 0 và 12 > 0. Nên – 5,6 < 12
g) Có 79 < 1 và 1,5 > 1. Nên 79 < 1,5.
Học tốt Tập hợp các số hữu tỉ
Các bài học để học tốt Tập hợp các số hữu tỉ Toán lớp 7 hay khác:
Xem thêm tóm tắt lý thuyết Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 7 hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn