Tính chất ba đường trung tuyến của tam giác (Lý thuyết Toán lớp 7) – Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác hay nhất, chi tiết sách Chân trời sáng tạo
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tính chất ba đường trung tuyến của tam giác (Lý thuyết Toán lớp 7) – Chân trời sáng tạo

Lý thuyết Tính chất ba đường trung tuyến của tam giác

1. Đường trung tuyến của tam giác

Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm cạnh đối diện.

Chú ý: mỗi tam giác có ba đường trung tuyến.

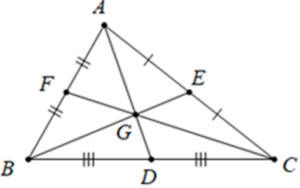
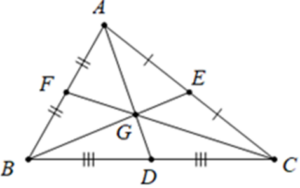
Ví dụ:Trong hình dưới đây, ba đường thẳng AD, BE, CF được gọi là ba đường trung tuyến của tam giác ABC.

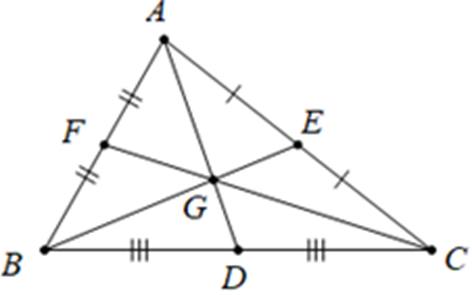
2. Tính chất ba đường trung tuyến của tam giác

Định lí: Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 23 độ dài đường trung tuyến đi qua đỉnh ấy.

Ví dụ: Trong hình vẽ dưới đây, các đường trung tuyến AD, BE, CF cùng đi qua điểm G. Điểm G gọi là trọng tâm của tam giác ABC.

Ta có: AGAD=BGBE=CGCF=23.

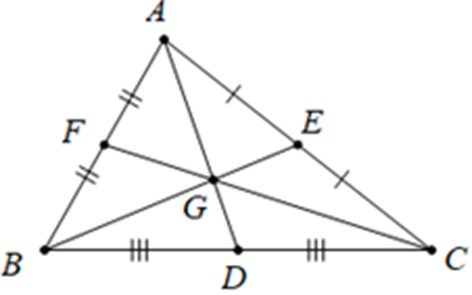
Bài tập Tính chất ba đường trung tuyến của tam giác

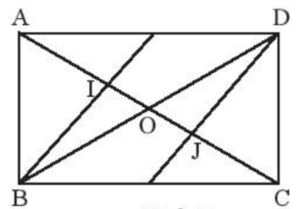
Bài 1: Cho hình chữ nhật ABCD, có I và J lần lượt là trọng tâm các tam giác ABD và CBD. Chứng minh AI = IJ = JC.

Hướng dẫn giải

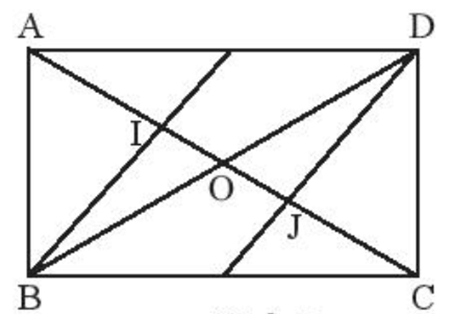
Gọi O là giao điểm hai đường chéo của hình chữ nhật, nên ta có AO = BO.

+) Ta có I là trọng tâm của tam giác ABD, suy ra:

AI=23AO;IO=AO-AI=13AO. (1)

+) Ta có J là trọng tâm của tam giác CBD, suy ra:

JC=23CO=23AO;OJ=CO-JC=13CO=13AO. (2)

Vậy suy ra IJ=IO+OJ=13AO+13AO=23AO. (3)

Từ (1), (2) và (3) suy ra: AI=IJ=IC=23AO.

Bài 2: Cho tam giác ABC có ba đường trung tuyến AD, BE, CF đồng quy tại G. Chứng minh: GA+GB+GC=23(AD+BE+CF).

Hướng dẫn giải

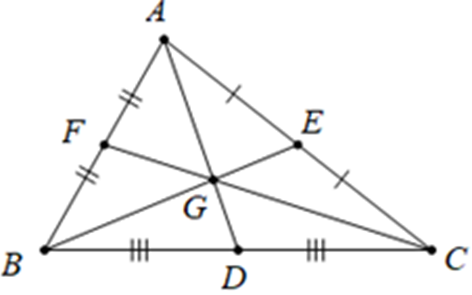
Trong tam giác ABC, các đường trung tuyến AD, BE, CF cùng đi qua điểm G. Điểm G gọi là trọng tâm của tam giác ABC.

Ta có: AGAD=BGBE=CGCF=23.

Suy ra GA=23AD;GB=23BE;GC=23CF.

Từ đó ta có: GA+GB+GC=23(AD+BE+CF).

Bài 3: Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G.

a) Biết BM = 9 cm, tính BG.

b) Biết GN = 2 cm, tính CN.

c) Tìm x biết BG = 3x, GM = x + 1.

Hướng dẫn giải

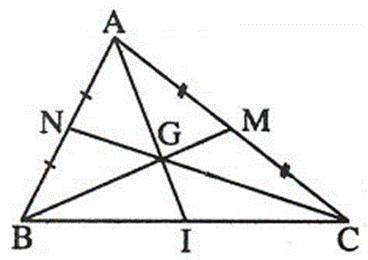
a) G là trọng tâm của tam giác ABC nên suy ra:

BG=23BM=23.9=6(cm).

b) G là trọng tâm của tam giác ABC nên suy ra: CG=23CN.

Từ đó GN=CN-CG=CN-23CN=13CN.

Hay: 2=13CN.

Vậy suy ra CN = 2.3 = 6 (cm).

c) Ta có: BM = BG + GM

Suy ra: 9 = 3x + (x + 1)

Hay 4x + 1 = 9

Tương đương với 4x = 9 – 1 = 8

Vậy suy ra: x = 8 : 4 = 2.

Học tốt Tính chất ba đường trung tuyến của tam giác

Các bài học để học tốt Tính chất ba đường trung tuyến của tam giác Toán lớp 7 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Xem thêm các tài liệu học tốt lớp 7 hay khác:

---