Tính chất đường phân giác của tam giác (Lý thuyết Toán lớp 8) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 8 Bài 17: Tính chất đường phân giác của tam giác sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Tính chất đường phân giác của tam giác (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Tính chất đường phân giác của tam giác

1. Tính chất đường phân giác của tam giác

Định lí: (Tính chất đường phân giác của tam giác) Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.

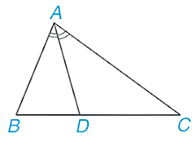
2. Chứng minh định lí

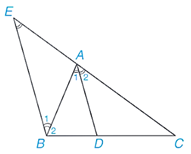
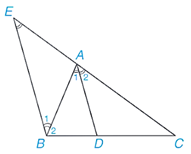
Vẽ đường thẳng qua B, song song với AD, cắt đường thẳng AC tại E.

Theo giả thiết, AD là phân giác của góc A nên A1^ = A2^  .

Ta có: EB // AD nên A1^ = B1^ (hai góc so le trong);

A2^ = E^ (hai góc đồng vị).

Do đó: 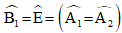  nên tam giác AEB cân tại A.

Suy ra: AE = AB (1).

Mặt khác, áp dụng định lí Thalès vào tam giác CEB, ta có:

 DBDC  =  AEAC(2).

Từ (1) và (2) ta suy ra: DBDC  =  ABAC .

Chú ý: Trong tam giác ABC, nếu D là điểm thuộc đoạn BC và thỏa mãn DBDC  =  ABAC  thì AD là đường phân giác của góc A.

Ví dụ: Tính độ dài x trong hình dưới đây biết AM là đường phân giác của góc A.

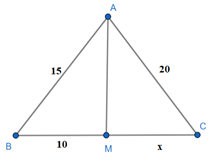
Hướng dẫn giải

Trong tam giác ABC có AM là đường phân giác của góc A.

Do đó ta có: 

MCMB  =  ACAB   hay   x10  =  2015.

Suy ra: x = 20 ⋅ 1015  =  403 .

Bài tập Tính chất đường phân giác của tam giác

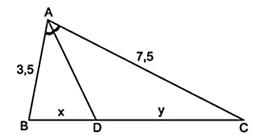
Bài 1: Cho hình vẽ dưới đây.

a) Tính xy .

b) Tính x khi y = 5.

Hướng dẫn giải

a) Từ hình vẽ ta có AD là đường phân giác của góc A trong tam giác ABC.

Dựa vào tính chất đường phân giác của tam giác, ta có

ABAC  =  BDDC  hay   3,57,5  =  xy.

Suy ra: xy  =  715 .

b) Khi y = 5 thì x = 5 ⋅ 715  =  73 .

Bài 2: Tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD và đường phân giác ngoài AE. Tính độ dài các đoạn thẳng DB, EB.

Hướng dẫn giải

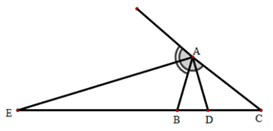
Vì AD là đường phân giác trong của tam giác ABC, nên ta có

 DBDC  =  ABAC(1)

AE là đường phân giác ngoài của tam giác ABC, ta có:

 EBEC  =  ABAC(2)

Từ (1) và (2) suy ra: DBDC  =   EBEC  =  ABAC  =  69  =  23 .

Từ DBDC=23 , suy ra DBBC  =  25 ⇒ DB = 25 BC = 25  . 10 = 4 (cm).

Từ EBEC=23 , suy ra EBBC=2  ⇒ EB = 2BC = 2 . 10 = 20 (cm).

Vậy DB = 4 cm và EB = 20 cm.

Học tốt Tính chất đường phân giác của tam giác

Các bài học để học tốt Tính chất đường phân giác của tam giác Toán lớp 8 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay khác:

Xem thêm các tài liệu học tốt lớp 8 hay khác:

---