Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết | Toán lớp 9 – Tóm tắt công thức Toán lớp 9 quan trọng đầy đủ, chi tiết giúp học sinh dễ dàng nhớ được công thức Toán 9.-Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết – Toán lớp 9
Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết – Toán lớp 9
Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết
Bài viết Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết Toán lớp 9 hay nhất gồm 2 phần: Lý thuyết và Các ví dụ
áp dụng công thức trong bài có lời giải chi tiết giúp học sinh dễ học, dễ nhớ Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết.
I. Lý thuyết
1. Định nghĩa về tiếp tuyến
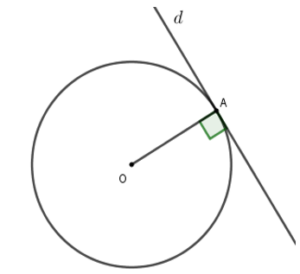
Nếu đường thẳng d và đường tròn (O) chỉ có một điểm chung với nhau là A thì ta nói d là tiếp tuyến của đường tròn (O). Điểm chung A đó gọi là tiếp điểm.
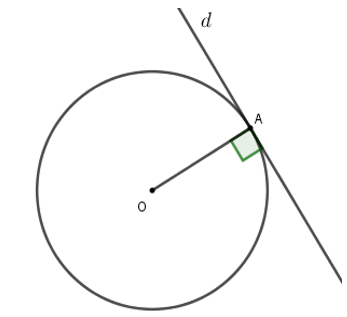
2. Tính chất của tiếp tuyến
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm của đường tròn đó.
3. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Dấu hiệu 1: Theo định nghĩa tiếp tuyến:
Đường thẳng chỉ có duy nhất một điểm chung với đường tròn là tiếp tuyến của đường tròn đó
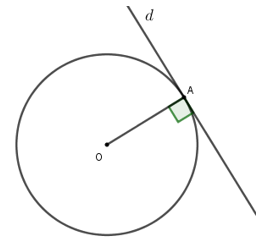
Đường thẳng d có duy nhất một điểm chung với đường tròn (O) là A nên d là tiếp tuyến của đường tròn
Dấu hiệu 2: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
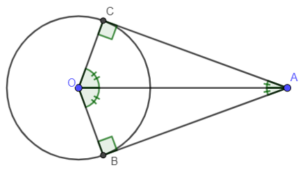
3. Tính chất hai tiếp tuyến cắt nhau
• Nếu hai tuyến tuyến của một đường tròn cắt nhau tại một điểm thì
– Điểm đó cách đều hai tiếp điểm.
– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
– Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua hai tiếp điểm.
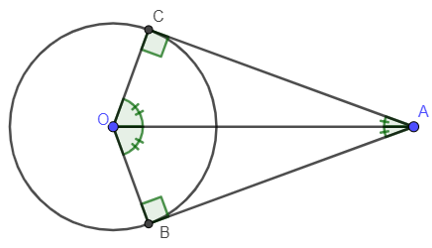
Cho đường tròn (O;R) có AB; AC là hai tiếp tuyến của đường tròn; B, C là hai tiếp điểm
Khi đó ta có:
+ AB = AC.
+ AO là tia phân giác BAC^ hay CAO^=BAO^=12BAC^.
+ OA là tia phân giác BOC^ hay BOA^=COA^=12BOC^.
II. Một số ví dụ:
Ví dụ 1: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là tiếp điểm).
a) Chứng minh AO vuông góc với MN.
b) Vẽ đường kính NOC. Chứng minh MC // AO.
c) Tính độ dài các cạnh tam giác AMN biết: OM = 3cm, OA = 5cm.
Lời giải:
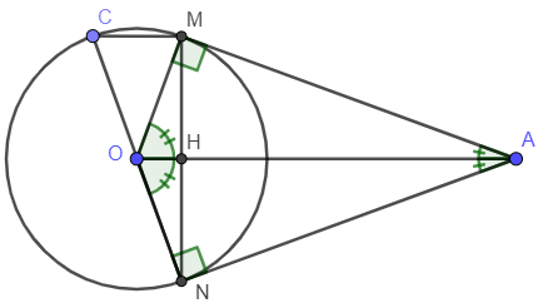
a) Gọi H là giao điểm của AO và MN.
Vì AM và AN là hai tiếp tuyến cắt nhau tại A nên OA là tia phân giác MON^
⇒MOA^=NOA^ (tính chất)
Xét tam giác OMH và tam giác ONH có:
OM = ON = R
OH chung
MOA^=NOA^ (chứng minh trên)
Do đó: ΔOMH=ΔONH(c – g – c)
⇒OHM^=OHN^ (hai góc tương ứng)
Mà OHM^+OHN^=180° (hai góc kề bù)
Do đó: OHM^=OHN^=90° hay OH⊥MN
⇒OA⊥MN (do H nằm trên OA)
b) Xét tam giác MNC có ba đỉnh M, N, C cùng nằm trên đường tròn (O)
Lại có NC là đường kính
Do đó tam giác MNC vuông tại M.
⇒MC⊥MN
Ta có:
MC⊥MNOA⊥MN⇒MC//OA (quan hệ từ vuông góc đến song song)
c) Xét tam giác OMA vuông tại M (do AM là tiếp tuyến của (O) với M là tiếp điểm) ta có:
OM2+MA2=OA2 (định lý Py – ta – go)
⇔32+MA2=52
⇔MA2=25−9
⇔MA2=16
⇔MA=4cm
Mà MA và NA là hai tiếp tuyến cắt nhau
⇒MA=NA=4cm (tính chất)
Tam giác OAM vuông tại M, đường cao MH ta có:
MA.MO = MH.OA
⇔4.3=MH.5
⇔5MH=12
⇔MH=12:5
⇔MH=2,4cm
Tam giác OMN có:
OM = ON
Do đó tam giác OMN cân tại O.
⇒ Khi đó OH vừa là đường cao vừa là đường trung tuyến.
Suy ra H là trung điểm của MN
MN = 2MH = 2,4.2 = 4,8cm
Vậy tam giác AMN có AM = AN = 4 cm, MN = 4,8 cm.
Ví dụ 2: Từ điểm A nằm ngoài đường tròn (O; R) kẻ hai tiếp tuyến AB, AC (với B và C là hai tiếp điểm). Kẻ BE vuông góc với AC, CF vuông góc với AB (E thuộc AC, F thuộc AB), BE và CF cắt nhau tại H.
a) Chứng minh tứ giác OBHC là hình thoi.
b) Chứng minh ba điểm A, H, O thẳng hàng.
Lời giải:
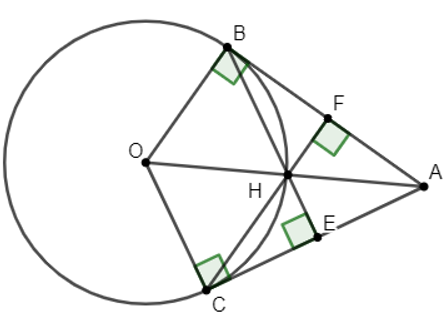
a) Vì AB là tiếp tuyến của đường tròn (O) tại B nên OB⊥AB
Lại có CF⊥AB (giải thuyết)
Do đó: OB // CF hay OB // CH (1)
Vì AC là tiếp tuyến của đường tròn (O) tại C nên OC⊥AC
Lại có: BE⊥AC (giả thuyết)
Do đó: OC // BE hay OC // BH (2)
Xét tứ giác OBHC có:
OB // CH (theo (1))
OC // BH (theo (2))
Do đó tứ giác OBHC là hình bình hành (dấu hiệu nhận biết)
Lại có: OB = OC nên hình bình hành OBHC là hình thoi (dấu hiệu nhận biết).
b) Vì OBHC là hình thoi nên OH là đường phân giác góc BOC^ (tính chất) (3)
Do AB, AC là hai tiếp tuyến của đường tròn (O) và chúng cắt nhau tại A
Nên OA là đường phân giác góc BOC^ (tính chất) (4)
Từ (3) và (4) ⇒OA≡OH hay O, A, H thẳng hàng.
Xem thêm các Công thức Toán lớp 9 quan trọng hay khác:


Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn