Tổng hợp Công thức Toán 11 (cả năm – sách mới) – Tổng hợp Công thức Toán 11 sách mới đầy đủ, chi tiết như một cuốn sổ tay công thức giúp bạn học tốt môn Toán 11.-Tổng hợp Công thức Toán 11 (cả năm – sách mới)
Tổng hợp Công thức Toán 11 (cả năm – sách mới)
Việc nhớ chính xác một công thức Toán 11 trong hàng trăm công thức không phải là việc dễ dàng. Bài viết tổng hợp kiến thức, công thức Toán 11 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều đầy đủ Học kì 1, Học kì 2 Đại số & Hình học như là cuốn sổ tay công thức giúp bạn học tốt môn Toán 11.
Tổng hợp Công thức Toán 11 (cả năm – sách mới)
Lưu trữ: Công thức Toán 11 (sách cũ)
Hi vọng với bài tóm tắt công thức Toán 11 này, học sinh sẽ dễ dàng nhớ được công thức và biết
cách làm các dạng bài tập Toán lớp 11. Mời các bạn đón xem:

I. HÀM SỐ LƯỢNG GIÁC
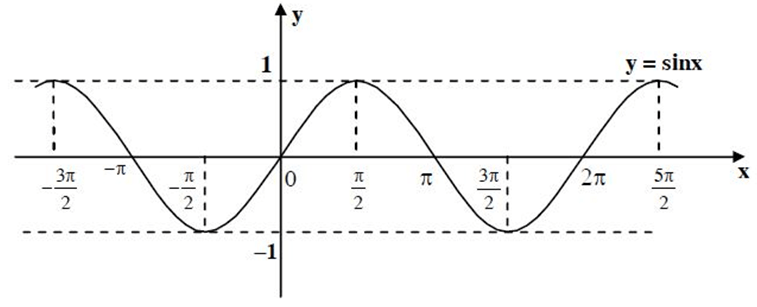
1. Hàm số y = sinx
– TXĐ: 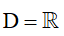 và -1 ≤ sinx ≤ 1 ,
và -1 ≤ sinx ≤ 1 ,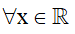
– Là hàm số lẻ
– Là hàm số tuần hoàn chu kì là 2π
– Hàm số đồng biến trên 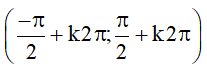
– Hàm số nghịch biến trên 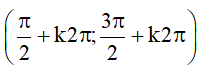
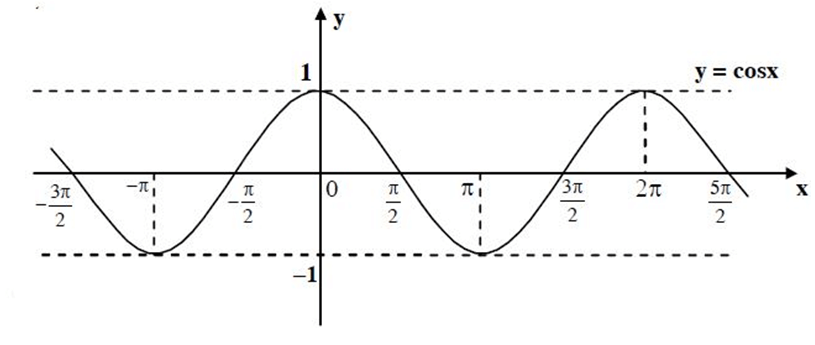
2. Hàm số y = cosx
– TXĐ: 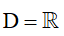 và -1 ≤ sinx ≤ 1 ,
và -1 ≤ sinx ≤ 1 ,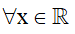
– Hàm số chẵn
– Là hàm số tuần hoàn chu kì là 2π
– Hàm số đồng biến trên (-π + k2π ; k2π)
– Hàm số nghịch biến trên (k2π ; π + k2π)
3. Hàm số y = tanx
-TXĐ: 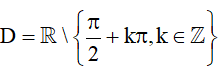
– Hàm số lẻ
– Là hàm số tuần hoàn chu kì là π
– Hàm số đồng biến trên 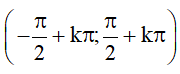
– Có các đường tiệm cận 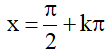
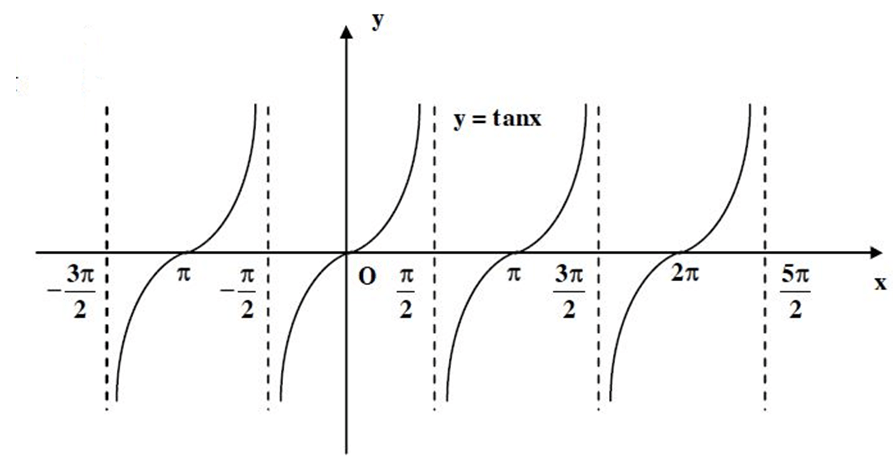
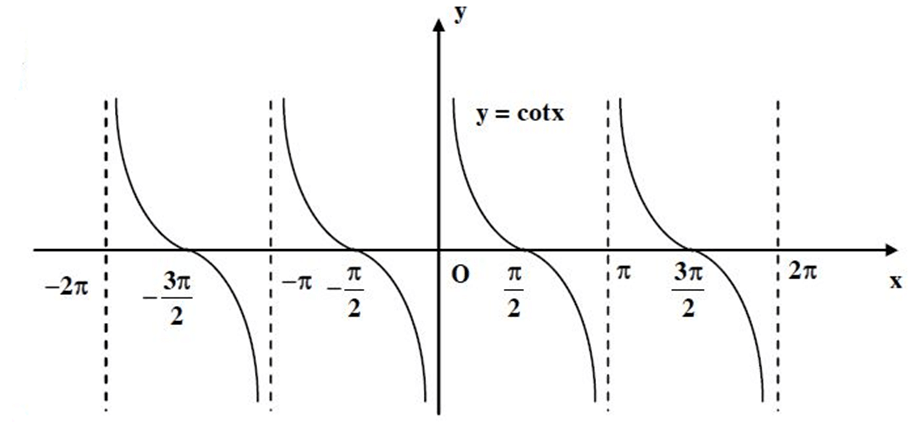
4. Hàm số y = cotx
– TXĐ: 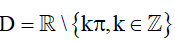
– Hàm số lẻ
– Là hàm số tuần hoàn chu kì là π
– Hàm số nghịch biến trong (kπ π + kπ)
– Có các đường tiệm cận x = kπ
II. CÔNG THỨC LƯỢNG GIÁC
+) Công thức lượng giác cơ bản:
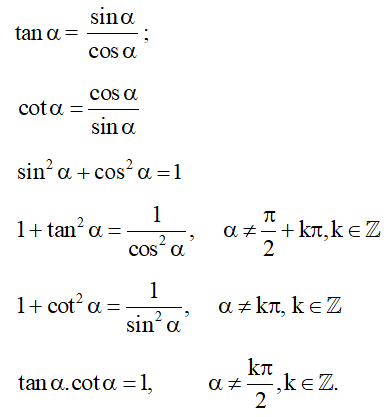
+) Giá trị lượng giác của các cung có liên quan đặc biệt.
– Cung đối nhau: α và -α
cos(-α ) = cos α
sin(-α ) = -sinα
tan(-α ) = -tanα
cot(-α ) = -cot α.
– Cung bù nhau: α và π – α
sin(π – α ) = sinα
cos(π – α ) = -cosα
tan(π – α ) = -tanα
cot(π – α ) = -cotα .
– Cung hơn kém π : α và (α + π)
sin(α + π) = -sinα
cos (α + π = -cosα
tan(α + π) = tanα
cot(α + π) = cotα
– Cung phụ nhau: α và 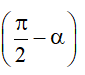
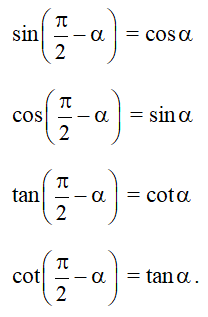
→ cos đối, sin bù, phụ chéo, hơn kém π tan và cot.
+) Hai cung hơn kém : 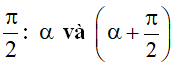
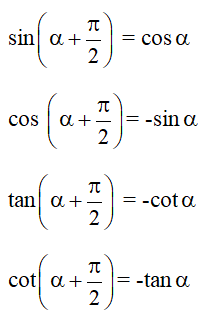
3. CÔNG THỨC LƯỢNG GIÁC
+) Công thức cộng
cos(a – b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb – sina sinb
sin(a – b) = sina cosb – cosa sinb
sin(a + b) = sina cosb + cosa sinb
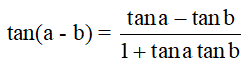
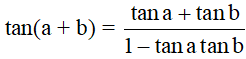
+) Công thức nhân đôi
sin2a = 2sina cosa
cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2
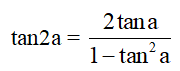
+) Công thức nhân ba
sin3a = 3sina – 4sin3a
cos3a = 4cos3a – 3cosa
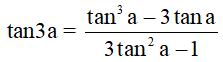
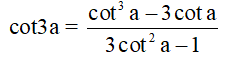
+) Công thức hạ bậc
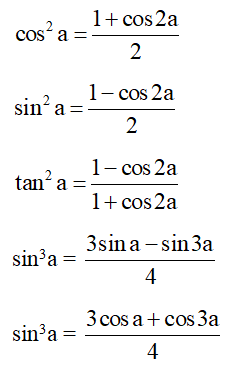
+) Các hệ quả
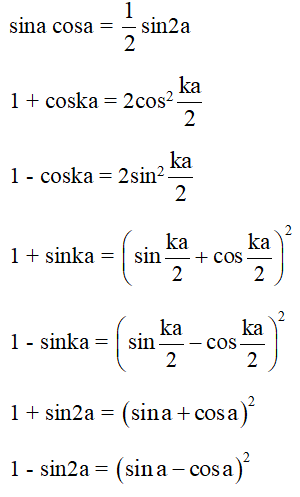
+) Công thức biến đổi tích thành tổng
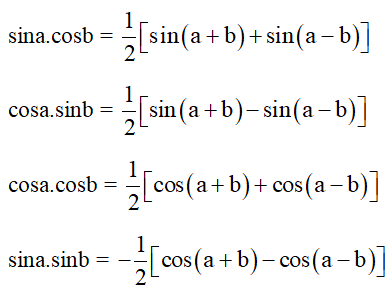
+) Công thức biến đổi tổng thành tích:
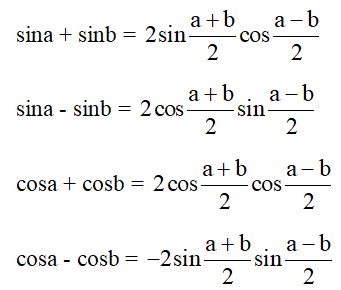
+) Đặc biệt khi a = b = α
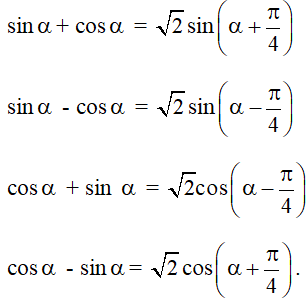
III. PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Phương trình lượng giác cơ bản
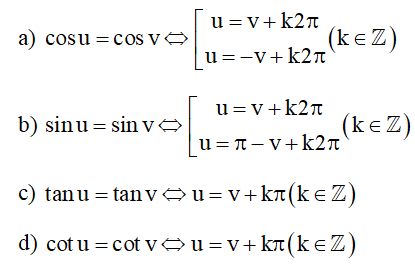
Đặc biệt:
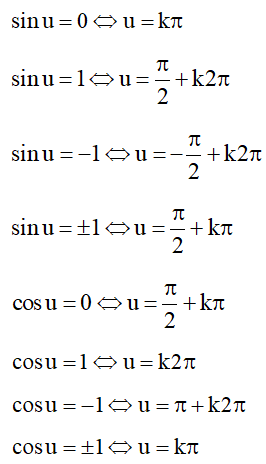
2. Phương trình bậc hai đối với một hàm số lượng giác
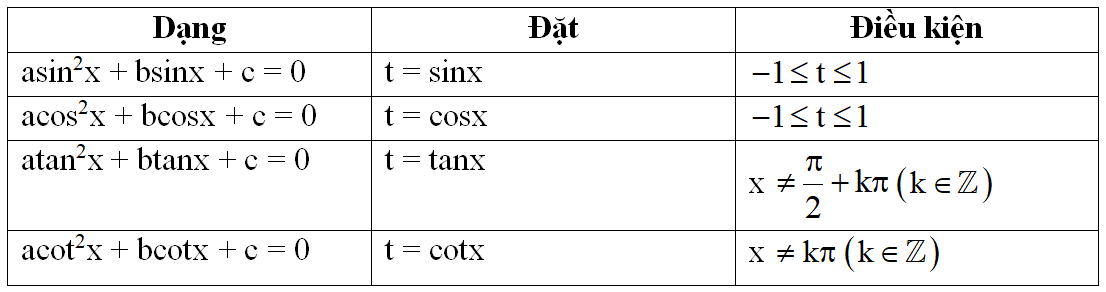
Giải lấy nghiệm t thích hợp sau đó áp dụng phương trình cơ bản
Chú ý: cos2x = 2cos2x – 1 = 1 – 2sin2x = cos2x – sin2x
sin2x = 1 – cos2x
cos2x = 1 – sin2x
3. Phương trình bậc nhất đối với sinx và cosx
– Dạng phương trình: asinx + bcosx = c
– Điều kiện có nghiệm: a2 + b2 ≥ c2
– Phương pháp giải: Chia 2 vế phương trình cho 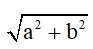 , sau đó áp dụng công thức cộng để đưa về dạng phương trình cơ bản.
, sau đó áp dụng công thức cộng để đưa về dạng phương trình cơ bản.
4. Phương trình đẳng cấp bậc hai đối với sinu và cosu
Dạng asin2u + bsinu.cosu + c.cos2u = d
Cách giải
+ Kiểm tra xem cosu = 0 có thỏa mãn phương trình hay không?
Xét 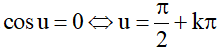
Thay cosu = 0 vào pt (nhớ sin2u = 1 )
+ Xét 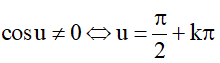
Chia 2 vế pt cho , giải pt theo .
Ghi chú: Có thể giải bằng cách dùng công thức hạ bậc đưa về dạng asin2u + bcos2u = c .
5. Phương trình đối xứng, phản đối xứng
– Dạng phương trình chứa sinu ± cosu và sinu.cosu
– Cách giải
Đặt 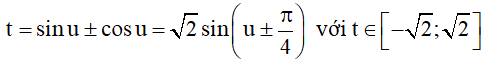
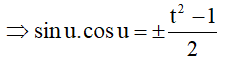
Thay vào phương trình đã cho ta được phương trình bậc hai theo t.
Chú ý:
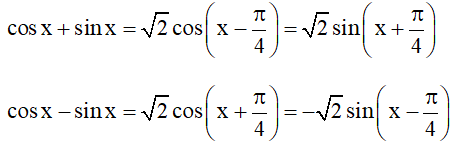
I. Đại số tổ hợp
1. Quy tắc cộng
Công việc chia làm 2 trường hợp:
– Trường hợp 1: có m cách.
– Trường hợp 2: có n cách.
Khi đó, tổng số cách thực hiện là .
2. Quy tắc nhân
Sự vật 1 có m cách. Ứng với 1 cách chọn trên ta có n cách chọn sự vật 2.
Khi đó, tất cả số cách chọn liên tiếp 2 sự vật là mn .
3. Giai thừa
n! = 1.2.3…(n -1)n
Qui ước: ): 0! = 1
Lưu ý:
n! = (n -1)!n = (n – 2)!(n – 1)n = …
4. Hoán vị
n vật sắp xếp vào n chỗ, số cách xếp là: Pn = n!
5. Chỉnh hợp
n vật, lấy ra k 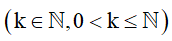 vật rồi sắp xếp thứ tự, số cách xếp là:
vật rồi sắp xếp thứ tự, số cách xếp là:
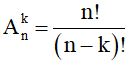
6. Tổ hợp
n vật, lấy ra 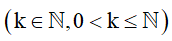 vật nhưng không sắp xếp thứ tự, số cách xếp là:
vật nhưng không sắp xếp thứ tự, số cách xếp là:
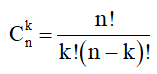
7. Một số kiến thức cần nhớ
Số chia hết cho 2 : tận cùng là 2 ; 4; 6; 8
Số chia hết cho 5 : tận cùng là 0;5
Số chia hết cho 10 : tận cùng là 0
Số chia hết cho 100 khi tận cùng là 00;25;50;75
Số chia hết cho 3 : tổng các chữ số chia hết cho 3 .
Số chia hết cho 9 : tổng các chữ số chia hết cho 9 .
Khi gặp bài tập số tự nhiên mà trong đó có liên quan số 0 nên chia trường hợp.
+) Tính chất

II. Nhị thức Newton
1. Khai triển nhị thức Newton
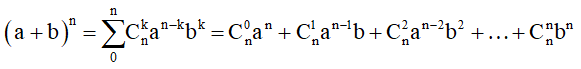
2. Một số công thức nên nhớ
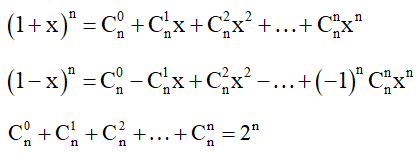
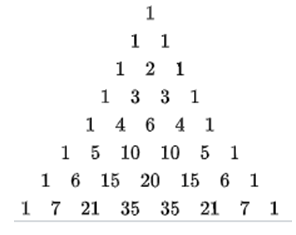
3. Tam giác Pacal (cho biết giá trị của 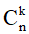 )
)
III. Xác suất
Không gian mẫu: Ω
Số phần tử của không gian mẫu: n(Ω)
1. Xác suất của biến cố A: 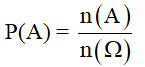
Lưu ý: 0 ≤ P(A) ≤ 1
2. A1; A2; …; Ak là các biến cố đôi một xung khắc thì
P(A1 ∪ A2 ∪…∪Ak) = P(A1) + P(A2) +…+ P(Ak)
3. A1; A2; …; Ak là các biến cố độc lập thì
P(A1A2…Ak) = P(A1)P(A2)…P(Ak)
4. 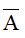 là biến cố đối của biến cố A thì:
là biến cố đối của biến cố A thì: 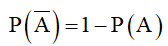
Hay ta có: 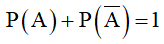
5. X là biến ngẫu nhiên rời rạc với tập giá trị là {x1; x2;…;xn}
a) Kỳ vọng của X là 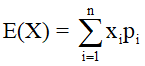 với pi = P(X = xi), i = 1,2,3,…,n
với pi = P(X = xi), i = 1,2,3,…,n
b) Phương sai của X là 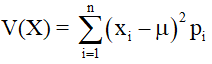 hay
hay 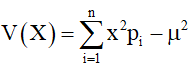 trong đó và pi = P(X = xi) , i = 1,2,3,…,n và μ = E(X)
trong đó và pi = P(X = xi) , i = 1,2,3,…,n và μ = E(X)
c) Độ lệch chuẩn: 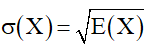
1. Đại cương về phép biến hình
PBH F : 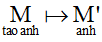 (biến M thành duy nhất một điểm M’ ), kí hiệu M’ = F(M)
(biến M thành duy nhất một điểm M’ ), kí hiệu M’ = F(M)
– Hình H’ = F(H) ⇔ H’ = 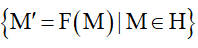
– O = F(O) ⇔ O là điểm bất động.
– PBH mà mọi điểm trong mặt phẳng đều biến thành chính nó được gọi là phép đồng nhất. Kí hiệu .
– 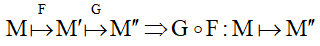 (tích hai PBH bằng cách thực hiện liên tiếp PBH F rồi G )
(tích hai PBH bằng cách thực hiện liên tiếp PBH F rồi G )
2. Phép dời hình
PBH F là PDH và A’ = F(A); B’ = F(B) thì A’B’ = AB (bảo toàn khoảng cách giữa hai điểm bất kì)
PDH biến
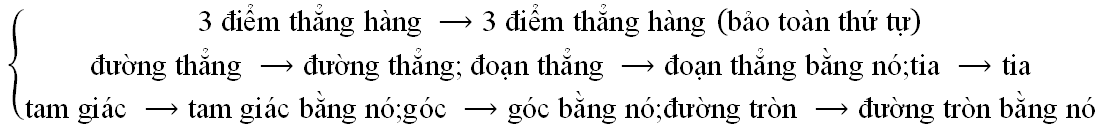
3. Phép tịnh tiến theo 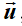 , kí hiệu
, kí hiệu 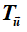
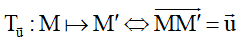
4. Phép đối xứng trục (ĐXTR) d , kí hiệu Đd
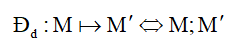 đối xứng nhau qua d
đối xứng nhau qua d
5. Phép đối xứng tâm (ĐXT) I , kí hiệu ĐI
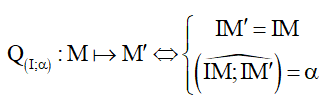
6. Phép vị tự (PVT) tâm I tỉ số k , kí hiệu V(I;k)
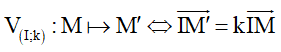
7. Phép đồng dạng (PĐD)
PĐD tỉ số k (k > 0) là PBH sao cho với hai điểm A;B bất kì và ảnh A’;B’ của nó ta có A’B’ = kAB
PĐD biến
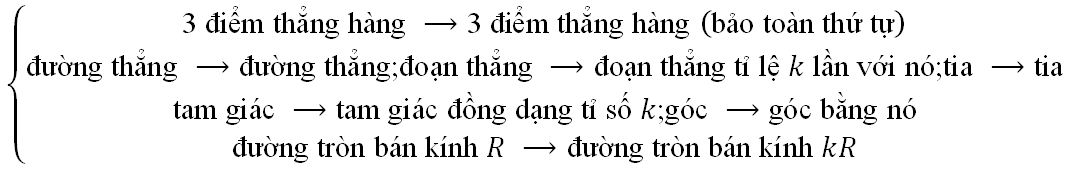
8. Biểu thức tọa độ
Giả sử M(x;y) , M(x’;y’) .
+) PTT theo 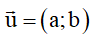 là
là 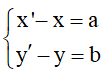
+) Phép đối xứng tâm I(a;b) là 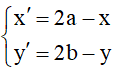
+) Phép đối xứng trục d khi 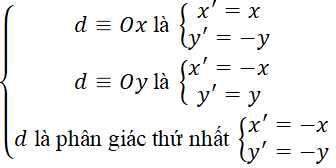
+) Phép quay tâm I(a;b) , góc α là 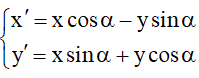
Đặc biệt: Tâm quay là O(0;0) thì
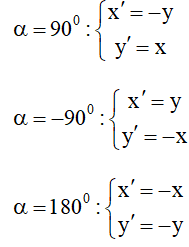
Phép vị tự tâm I(a;b) , tỉ số k là 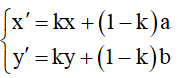
9. Ảnh của đường thẳng d qua PTT; phép ĐXT; PQ; PVT
Giả sử F: 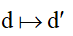 ( F ở đây là
( F ở đây là 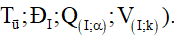 ). Lấy M(x;y) ∈ d . Giả sử F:
). Lấy M(x;y) ∈ d . Giả sử F: 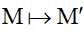 với M'(x’;y’)
với M'(x’;y’)
Viết biểu thức tọa độ tương ứng với PBH đề cho ⇒ 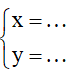
Ta có M ∈ d (thay x;y vào đường thẳng d ) ta được đường thẳng d’ .
10. Ảnh của đường tròn
Giả sử F: 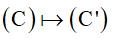 ( ở đây là
( ở đây là 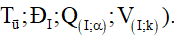 )
)
Xác định tâm I của đường tròn (C) . Tìm ảnh I’ của I qua PBH F .
Ta có: 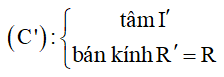 (riêng phép vị tự thì
(riêng phép vị tự thì 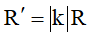 ). Từ đó ta có phương trình (C’) .
). Từ đó ta có phương trình (C’) .
11. Tâm vị tự của hai đường tròn
TH1: Nếu I ≡ I’ thì PVT tâm O ≡ I, tỉ số 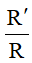 và PVT tâm O ≡ I, tỉ số
và PVT tâm O ≡ I, tỉ số 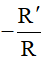 .
.
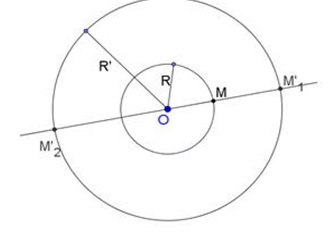
TH2: Nếu I ≠ I’ và R ≠ R’ thì PVT tâm O1 (tâm vị tự ngoài), tỉ số 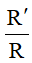 và PVT tâm O2 (tâm vị tự trong), tỉ số
và PVT tâm O2 (tâm vị tự trong), tỉ số 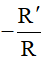 .
.
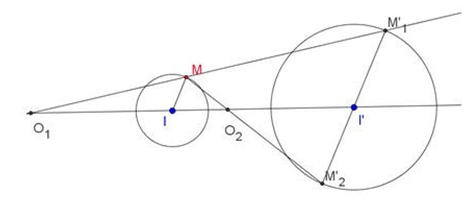
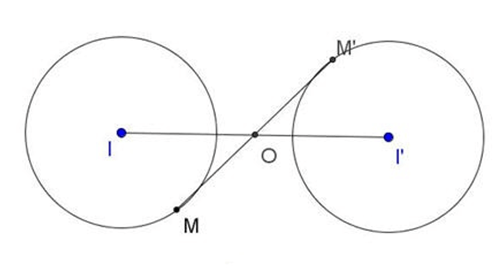
TH3: Nếu I ≠ I’ và R = R’ thì PVT tâm O, tỉ số k = 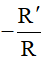 = -1
= -1



Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn