Nội dung bài viết
Tổng hợp lý thuyết Chương 4: Số phức lớp 12 (hay, chi tiết) – Tổng hợp các dạng bài tập Toán 12 với phương pháp giải chi tiết giúp bạn biết các làm bài tập Toán 12.-Tổng hợp lý thuyết Chương 4: Số phức
Tổng hợp lý thuyết Chương 4: Số phức
Tổng hợp lý thuyết Chương 4: Số phức
Dưới đây là phần tổng hợp kiến thức, công thức, lý thuyết Toán lớp 12 Chương 4: Số phức ngắn gọn, chi tiết. Hi vọng tài liệu Lý thuyết Toán lớp 12 theo chương này sẽ giúp bạn nắm vững kiến thức môn Toán lớp 12.
Lý thuyết Số phức
1. Phần thực và phần ảo của số phức, số phức liên hợp.
a) Số phức z là biểu thức có dạng z = a + bi (a, b ∈ R, i2 = -1) . Khi đó:
+ Phần thực của z là a, phần ảo của z là b và i được gọi là đơn vị ảo.
b) Số phức liên hợp của z là 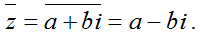 .
.
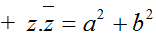
+ Tổng và tích của z và z− luôn là một số thực.
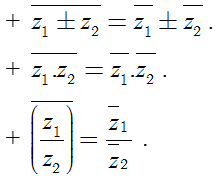
Đặc biệt:
+ Số phức z = a + 0i có phần ảo bằng 0 được coi là số thực và viết là z = a
+ Số phức z = 0 + bi có phần thực bằng 0 được gọi là số ảo (hay số thần ảo) và viết là
+ Số i = 0 + li = li.
+ Số: 0 = 0 + 0i vừa là số thực vừa là số ảo.
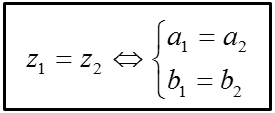
2. Số phức bằng nhau.
+ Cho hai số phức z1 = a1 + b1i, z2 + b2i (a1, a2, b1, b2 ∈ R). Khi đó:
3. Biểu diễn hình học của số phức, mô đun của số phức.
a) Biễu diễn hình học của số phức.
+ Số phức z = a + bi (a, b ∈ R) được biểu diễn bởi điểm M(a; b) trong mặt phẳng tọa độ.
+ z và z− được biểu diễn bởi hai điểm đối xứng nhau qua trục 0x.
b) Mô đun của số phức.
+ Mô đun của số phức z là 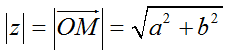 .
.
+ 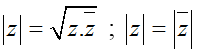
Lý thuyết Cộng, trừ và nhân số phức
Cho hai số phức z1 = a + bi và z2 = c + di thì:
•Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i
•Phép trừ số phức: z1 – z2 = (a – c) + (b – d)i
– Mọi số phức z = a + bi thì số đối của z là -z = -a – bi: z + (-z) = (-z) + z = 0
•Phép nhân số phức: z1.z2 = (ac – bd) + (ad + bc)i
•Phép chia số phức: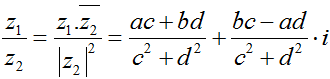 (với z2 ≠ 0)
(với z2 ≠ 0)
–Chú ý :
• Với mọi số thực k và mọi số phức z = a + bi thì:
k(a + b)i = ka + kbi
• Với mọi số phức: 0z = 0
• Phép cộng và phép nhân các số phức có tất cả các tính chất của phép cộng và phép nhân của số thực.
• i4k = 1; i4k + 1 = i; i4k + 2 = -1; i4k + 3 = -i
Ví dụ 1: Cho số phức z = 2 + 5i . Tìm số phức w = iz + z−.
A. w = 7 – 3i. B. w = -3 – 3i. C. w = 3 = 3i. D. w = -7 – 7i.
Lời giải:
Ta có: 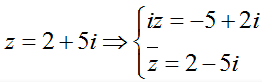 ⇔ w = iz + z− = (-5 + 2) + (2 – 5)i = -3 – 3i.
⇔ w = iz + z− = (-5 + 2) + (2 – 5)i = -3 – 3i.
Vậy chọn đáp án B.
Ví dụ 2: Cho số phức z = (1 – 6i) – (2 – 4i). Phần thực, phần ảo của z lần lượt là
A. -1; -2. B. 1; 2. C. 2;1. D. – 2;1.
Lời giải:
Ta có : z = (1 – 6i) – (2 – 4i) = -1 -2i
Vậy chọn đáp án A.
Ví dụ 3: Cho số phức z = (2 + i)(1 – i) + 1 + 3i. Tính môđun của z.
A. 4√2. B. √13. C. 2√2. D. 2√5.
Lời giải:
Ta có: z = (2 + i)(1 – i) + 1 + 3i = (2.1 + 1.1) + (-1.2 + 1.1)i + 1 + 3i = 4 + 2i
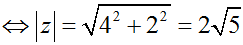 . Vậy chọn đáp án D.
. Vậy chọn đáp án D.
Lý thuyết Phép chia số phức
Cho hai số phức z1 = a + bi và z2 = c + di thì:
– Số phức nghịch đảo của z = a + bi ≠ 0: 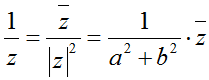
– 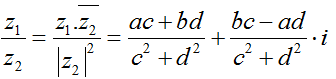 (với z2 ≠ 0)
(với z2 ≠ 0)
Ví dụ 1: Số phức nghịch đảo của có phần ảo là:
A. 1 B. 1/2 C. -1 D. -1/2
Lời giải:
Chọn D.
Ta có: 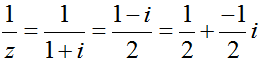
Ví dụ 2: Phần thực của số phức 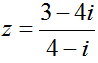 bằng
bằng
A. 16/17 B. 3/4 C. -13/17 D. -3/4
Lời giải:
Chọn A.
Ta có: 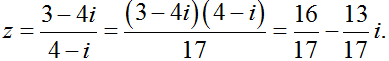
Ví dụ 3: Số phức 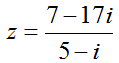 có phần thực là
có phần thực là
A. 3 B. 9/13 C. 2 D. -3
Lời giải:
Chọn C.
Ta có: 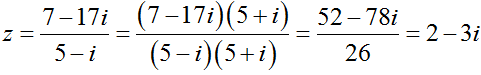
⇒ Phần thực của z là: 2
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi tốt nghiệp THPT khác:

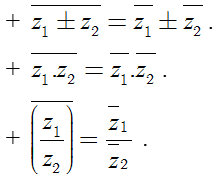

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn