Top 30 Đề thi Toán 9 Giữa kì 1 năm 2024 (có đáp án) – Bộ 100 Đề thi Toán 9 năm học 2024 – 2025 học kì 1, học kì 2 chọn lọc, có đáp án giúp bạn ôn tập đạt điểm cao trong các bài thi Toán 9.-Top 30 Đề thi Toán 9 Giữa kì 1 năm 2024 (có đáp án)
Top 30 Đề thi Toán 9 Giữa kì 1 năm 2024 (có đáp án)
Trọn bộ 30 đề thi Toán 9 Giữa kì 1 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều có đáp án và ma trận
sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 9.
Top 30 Đề thi Toán 9 Giữa kì 1 năm 2024 (có đáp án)
Xem thử Đề thi GK1 Toán 9 KNTT
Xem thử Đề thi GK1 Toán 9 CTST
Xem thử Đề thi GK1 Toán 9 CD
Chỉ từ 150k mua trọn bộ đề thi Toán 9 Giữa kì 1 bản word có lời giải chi tiết, dễ dàng chỉnh sửa:
Xem thử Đề thi GK1 Toán 9 KNTT
Xem thử Đề thi GK1 Toán 9 CTST
Xem thử Đề thi GK1 Toán 9 CD
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 1 – Kết nối tri thức
Năm học 2024 – 2025
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Cặp số nào sau đây không phải là nghiệm của phương trình 2x – y – 1 = 0?
A. (1; 1).
B. (2; 3).
C. (1; –2).
D. (0; –1).
Câu 2. Hệ phương trình ax+by=ca’x+b’y=c’ có nhiều nhất bao nhiêu nghiệm?
A. 0.
B. 1.
C. 2.
D. Vô số.
Câu 3. Cho tam giác ABC vuông tại A có đường cao AH. Khi đó HAHB bằng
A. sinC.
B. cosC.
C. tanC.
D. cotC.
Câu 4. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90° và sinα = 0,5. Khẳng định nào sau đây là đúng?
A. sinβ = 0,5.
B. cosβ = 0,5.
C. tanβ = 0,5.
D. cotβ = 0,5.
Phần 2. Câu trắc nghiệm đúng sai
Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 5. Cho ba số a, b, c thỏa mãn a > b và c < 0.
a) ac < bc.
b) ac>bc.
c) 2a – c > 2b – c.
d) c – 3a > c – 3b.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 6. Xác định hàm số y = ax + b để đồ thị của nó đi qua hai điểm A(–2; –1) và B(1; 4).
Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và AC = 11 cm. Số đo góc B được làm tròn đến phút là bao nhiêu?
B. TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm) Giải các phương trình và bất phương trình sau:
a) (2x + 5)(1 – 4x) = 0.
b) x+4x+1−x+1x−4=15xx2−3x−4.
c) 13 – 5x > –3x + 9.
d) x+13+2x+14≤5x+36+7+12×12.
Bài 2. (2,5 điểm)
a) Tìm các hệ số x và y trong phản ứng hóa học đã được cân bằng sau:
xFe3O4 + O2 → yFe2O3.
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
b) Giải bài toán sau bằng cách lập hệ phương trình:
Khi cho hai vòi nước cùng chảy vào một bể cạn thì sau 1 giờ 20 phút sẽ đầy bể. Nếu mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì sẽ được 215 bể. Hỏi nếu chảy riêng, mỗi vòi nước sẽ chảy đầy bể trong bao lâu?
Bài 3. (2,5 điểm)
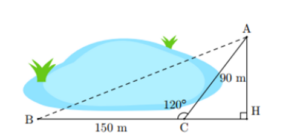
1) Bạn An muốn tính khoảng cách AB (làm tròn đến hàng phần mười của mét) ở hai bên hồ nước (hình vẽ). Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và bạn ấy dùng giác kế đo được ACB^=120°. Hãy tính AB giúp bạn An.
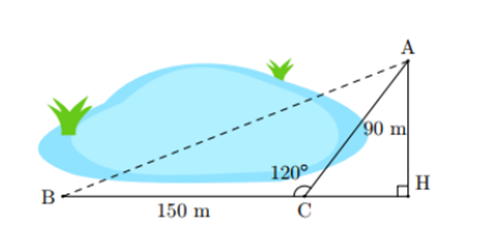
2) Cho tam giác ABC vuông tại A có đường cao AH (H ∈ BC).
a) Biết AC = 4 cm và C^=40°. Tính độ dài đường cao AH, cạnh AB và BC (làm tròn kết quả đến hàng phần trăm của cm).
b) Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N. Chứng minh rằng tan3C=BMCN.
—–HẾT—–
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 1 – Chân trời sáng tạo
Năm học 2024 – 2025
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (4,0 điểm)
Phần 1. Câu trắc nghiệm đúng sai
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 1. Cho phương trình 2x – 5y = 1 (*)
|
| Đúng | Sai |
| a) Cặp số (-2;1) là nghiệm của phương trình (*). |
|
|
| b) Phương trình (*) là phương trình bậc nhất hai ẩn có vô số nghiệm. |
|
|
| c) Hệ số a; b; c của phương trình (*) lần lượt là 2; 5; 1. |
|
|
| d) Tập hợp các điểm có tọa độ (x;y) thỏa mãn phương trình (*) là một đường thẳng |
|
|
Phần 2. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 2 đến câu 7, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 2. Điều kiện xác định của phương trình 1x−2+xx+1=−12 là
A. x ≠ 2.
B. x ≠ -1.
C. x ≠ 2 và x ≠ -1.
D. x ≠ 2 và x ≠ 0.
Câu 3. Cặp số nào sau đây là nghiệm của hệ phương trình 2x+3y=3−4x−5y=9?
A. (1;1).
B. (-21;15).
C. (1;-1).
D. (21;-15).
Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. x + y > 8.
B. 0x + 5 ≥ 0.
C. 2x – 3 > 4.
D. x2 – 6x + 1 ≤ 0.
| Câu 5. Biển báo giao thông trong hình bên báo đường cấm các xe cơ giới và thô sơ (kể cả các xe được ưu tiên theo quy định) có độ dài toàn bộ kể cả xe và hàng lớn hơn trị số ghi trên biển đi qua. Nếu xe có chiều rộng lớn hơn 3,2m thì không được phép lưu thông để đảm bảo an toàn cho cả xe và các phương tiện khác, cũng như tránh gây cản trở giao thông. Nếu một xe tải đi trên đường đó có chiều rộng a (m) thỏa mãn điều kiện gì? |
|
A. a = 3,2.
B. a > 3,2.
C. a > 3,2.
D. a ≤ 3,2.
Câu 6. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90° và α = 0,5. Khẳng định nào sau đây là đúng?
A. cos β = 0,5.
B. sin β = 0,5.
C. tan β = 0,5.
D. cot β = 0,5.
Câu 7. Cho tam giác ABC vuông tại A. Hệ thức nào sau đây là sai?
A. BC = ACsinB.
B. BC = ABsinC.
C. BC = ACcosC.
D. BC = ACtanC.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 8 và câu 10, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 8. Nghiệm lớn nhất của phương trình (4 – 2x)(x + 1) là bao nhiêu?
Câu 9. Số nguyên nhỏ nhất thỏa mãn bất phương trình x(5x + 1) + 4(x + 3) ≥ 5x2 là bao nhiêu?
Câu 10. Biết 0° < α < 90° tính giá trị biểu thức A = sinα+3cos90°−αsinα−2cos90°−α.
B. TỰ LUẬN (6,0 điểm)
Bài 1. (2,0 điểm) Giải các phương trình và bất phương trình sau:
a) x−1x+2−xx−2=4−6xx2−4;
b) 4x−12+6x−196≥9x−113.
Bài 2. (2,5 điểm)
1. Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại 180 ml nặng trung bình 10kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5,25 tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng 65 kg?
2. Giải bài toán sau bằng cách lập hệ phương trình:
Do ảnh hưởng của dịch Covid – 19 nên trong tháng hai cả hai tổ công nhân chỉ làm được 700 sản phẩm. Sang tháng ba, tình hình dịch ổn định tổ I vượt mức 20% tổ II vượt mức 15% nên cả hai tổ làm được 830 sản phẩm. Hỏi trong tháng hai mỗi tổ làm được bao nhiêu sản phẩm?
Bài 3. (2,0 điểm) Lúc 6 giờ sáng, bạn An đi từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc đỉnh C được mô tả như hình vẽ dưới. Cho biết đoạn AB dài 762 m, A ^=4°, B ^=6°.

a) Tính chiều cao con dốc (làm tròn kết quả đến hàng đơn vị của mét).
b) Hỏi bạn An đến trường lúc mấy giờ (làm tròn kết quả đến phút)? Biết rằng tốc độ lên dốc là 4 km/h và tốc độ xuống dốc là 19 km/h.
Bài 4. (0,5 điểm) Cho x, y là hai số thực thỏa mãn điều kiện x2 + 2y2 + 2xy + 7x + 7y + 10 = 0.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2x+2y−3x+y+6.
—–HẾT—–
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 1 – Cánh diều
Năm học 2024 – 2025
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Mẫu thức chung khi quy đồng mẫu thức của phương trình 1x−1+3×2−1+x=0 là
A. (x – 1)2.
B. (x + 1)2.
C. (x – 1)(x + 1).
D. x(x – 1)(x + 1).
Câu 2. Cho hệ phương trình 12x−12y=−1−3x+3y=5. Cho các khẳng định sau:
(i) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 6y = –1.
(ii) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 0x = –1.
(iii) Hệ phương trình đã cho vô nghiệm.
Số khẳng định đúng trong các khẳng định trên là
A. 0.
B. 1.
C. 2.
D. 3.
Câu 3. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?
A. sinB=ca.
B. c=bcotB.
C. b = c.cosC.
D. c = b.tanC.
Câu 4. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng?
A. AB2 = BC2 + AC2.
B. sinC = cosB.
C. cotB – tanB = 0.
D. cotC=ACAB.
Phần 2. Câu trắc nghiệm đúng sai
Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 5. Cho bất đẳng thức –5a > 3.
a) Số a có giá trị là một số âm.
b) Biểu thức 3 – 5a có giá trị là một số dương.
c) Biểu thức a+35 có giá trị là một số dương.
d) Biểu thức –10a – 10 có giá trị là một số âm.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 6. Tìm nghiệm của hệ phương trình 32x−y−6x+y=−112x−y−1x+y=0.
Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và đường cao AH = 3 cm. Tính số đo góc C (làm tròn kết quả đến phút).
B. TỰ LUẬN (7,0 điểm)
Bài 1. (2,5 điểm)
1. Giải các phương trình sau:
a) 4x(x + 3) – 3x – 9 = 0.
b) x+2x−2=x−2x+2+16×2−4.
2. Giải các bất phương trình sau:
a) 3x – 8 < 4x – 12.
b) 3(x – 2) – 5 > 3(2x – 1).
c) 4x−12+6x−196≥9x−113.
Bài 2. (2,0 điểm)
1. Xác định a và b sao cho hệ phương trình ax+2by=−18bx−3ay=−3 nhận cặp số (–3; 2) làm nghiệm.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.
Bài 3. (2,0 điểm)
1. Cho hình vẽ bên. Tính số đo góc α và các độ dài x, y (góc làm tròn đến độ và độ dài làm tròn đến hàng phần trăm).
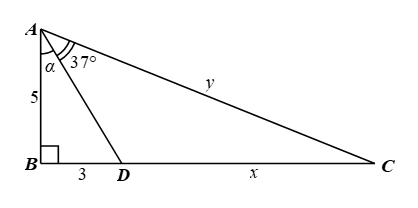
2. Tính chiều cao của một ngọn núi (kết quả làm tròn đến hàng đơn vị), biết tại hai điểm A, B cách nhau 500 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34° và 38° (hình vẽ).
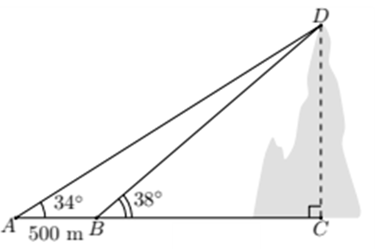
Bài 4. (0,5 điểm) Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo, chứng minh rằng:
SABCD=12AC⋅BD⋅sinα.
—–HẾT—–
Xem thử Đề thi GK1 Toán 9 KNTT
Xem thử Đề thi GK1 Toán 9 CTST
Xem thử Đề thi GK1 Toán 9 CD
Lưu trữ: Đề thi Giữa kì 1 Toán 9 (sách cũ)
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa học kì 1
Môn: Toán 9
Thời gian làm bài: 90 phút
(Đề 1)
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
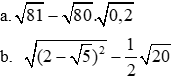
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
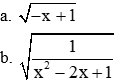
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
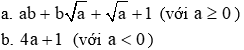
2. Giải phương trình: 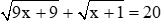
Bài 3 (2,0 điểm. Cho biểu thức:
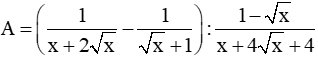
(với x > 0; x ≠ 1)
a. Rút gọn biểu thức A.
b. Tìm x để 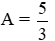
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng: 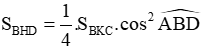
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 – 3(x + y) + 1993. Tính giá trị biểu thức P với:
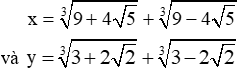
Bài 1.
1. Thực hiện phép tính
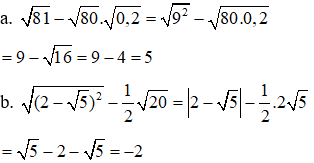
2. Tìm điều kiện của x để biểu thức có nghĩa
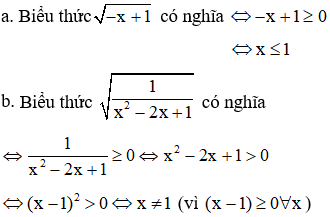
Bài 2.
1. Phân tích đa thức thành nhân tử:
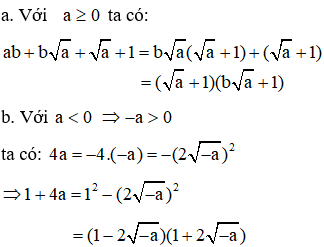
2. Giải phương trình
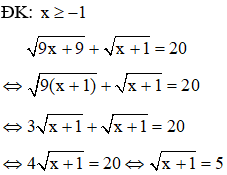
⇔ x + 1 = 25 ⇔ x = 24 (thỏa mãn điều kiện xác định)
Vậy phương trình có nghiệm duy nhất x = 24
Bài 3.
a. Rút gọn biểu thức
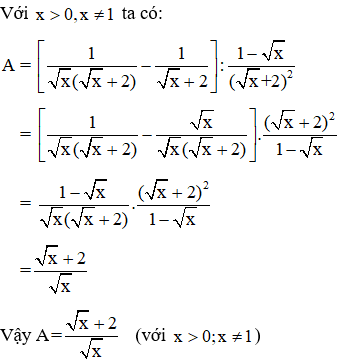
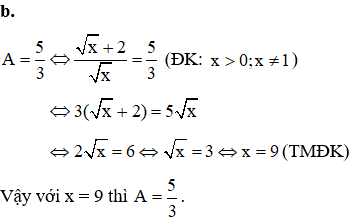
Bài 4.
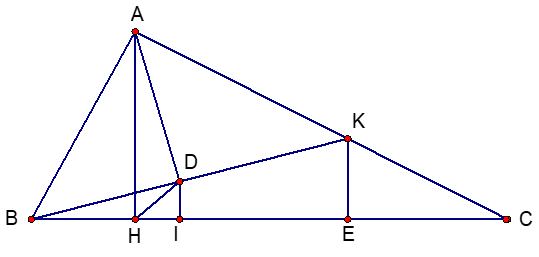
a.
Ta có ΔABC vuông tại A, đường cao AH
⇒ AB2 = BH.BC = 2.8 = 16 (hệ thức lượng trong tam giác vuông)
⇒ AB = 4cm (Vì AB > 0)
Mà BC2 = AB2 + AC2 (Định lý Pitago trong tam giác vuông ABC)
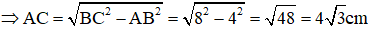
Có HB + HC = BC ⇒ HC = BC – HB = 8 – 2 = 6 cm
Mà AH2 = BH.CH = 2.6 = 12 (hệ thức lượng trong tam giác vuông)
⇒ 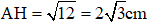 (Vì AH > 0)
(Vì AH > 0)
b.
Ta có ΔABK vuông tại A có đường cao AD
⇒ AB2 = BD.BK (1)
Mà AB2 = BH.BC (chứng minh câu a) (2)
Từ (1) và (2) suy ra BD.BK = BH.BC
c.

Bài 5.
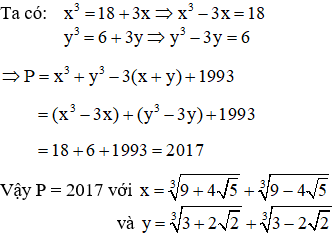
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa học kì 1
Môn: Toán 9
Thời gian làm bài: 90 phút
(Đề 2)
Bài 1 (2,5 điểm). Cho biểu thức:
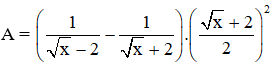
a) Rút gọn biểu thức
b) Tìm giá trị của x để A = 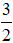
Bài 2 (2 điểm). Thực hiện phép tính:
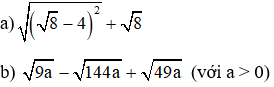
Bài 3 (2 điểm). Giải phương trình:
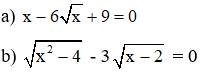
Bài 4 (3,5 điểm). Cho tam giác ABC có cạnh AB = 12cm, AC = 16cm, BC = 20cm. Kẻ đường cao AM. Kẻ ME vuông góc với AB.
a) Chứng minh tam giác ABC là tam giác vuông.
b) Tính độ dài AM, BM.
c) Chứng minh AE.AB = AC2 – MC2
d) Chứng minh AE.AB = MB.MC = EM.AC
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa học kì 1
Môn: Toán 9
Thời gian làm bài: 90 phút
(Đề 3)
Bài 1. (2 điểm) Tính giá trị của biểu thức:
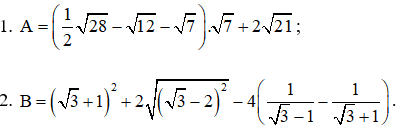
Bài 2.(2 điểm) Cho biểu thức:
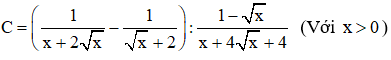
1. Rút gọn C;
2. Tìm x để 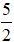 .
.
Bài 3.(2 điểm) Giải phương trình
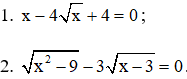
Bài 4.(3,5 điểm) Cho tam giác ABC vuông tại A có đường cao AH. Độ dài BH = 4cm và HC = 6cm.
1. Tính độ dài các đoạn AH, AB, AC.
2. Gọi M là trung điểm của AC. Tính số do góc AMB (làm tròn đến độ).
3. Kẻ AK vuông góc với BM (K ∈ BM). Chứng minh: ΔBKC đồng dạng với ΔBHM.
Bài 5.(0,5 điểm) Cho biểu thức: P = x3 + y3 – 3(x + y) + 2020
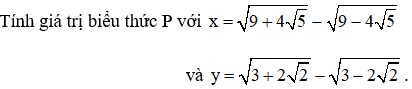
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa học kì 1
Môn: Toán 9
Thời gian làm bài: 90 phút
(Đề 4)
Bài 1 (1,5 điểm). Tính giá trị của các biểu thức sau:
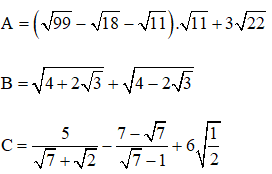
Bài 2 (2 điểm). Giải các phương trình sau:
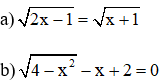
Bài 3 (2,5 điểm). Cho biểu thức:
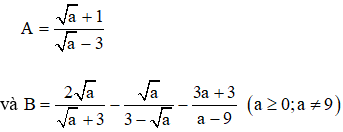
a) Tính giá trị của A khi a = 16
b) Rút gọn biểu thức 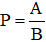
c) So sánh P với 1
Bài 4 (3,5 điểm).
1. (1 điểm)
Một chiếc tivi hình chữ nhật màn hình phẳng 75 inch (đường chéo tivi dài 75 inch) vói góc tạo bởi chiều rộng và đường chéo là 53°08′. Hỏi chiếc ti vi ấy có chiều dài, chiều rộng là bao nhiêu? Biết 1 inch = 2,54cm (kết quả làm tròn đến chữ số thập phân thứ nhất).
2. (2,5 điểm)
Cho tam giác EMF vuông tại M có đường cao MI. Vẽ IP vuông góc với ME (P thuộc ME), IQ vuông góc với MF (Q thuộc MF).
a) Cho biết ME = 4cm, 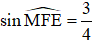 . Tính độ dài các đoạn EF, EI, MI.
. Tính độ dài các đoạn EF, EI, MI.
b) Chứng minh: MP.PE + MQ.QF = MI2
Bài 5 (0,5 điểm).
Tìm giá trị nhỏ nhất của biểu thức 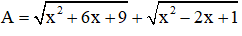
Xem thêm bộ đề thi Toán 9 năm học 2024 – 2025 chọn lọc khác:





Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn