Tứ giác (Lý thuyết Toán lớp 8) – Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 8 Bài 2: Tứ giác sách Chân trời sáng tạo hay nhất, chi tiết
sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Tứ giác (Lý thuyết Toán lớp 8) – Chân trời sáng tạo

Lý thuyết Tứ giác

1. Tứ giác

1.1. Tứ giác

Định nghĩa tứ giác:

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

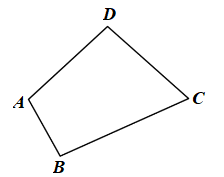
Đỉnh và cạnh của tứ giác:

– Tứ giác ABCD còn được gọi là tứ giác ADCB, BADC, BCDA, CBAD, CDAB, DCBA, DABC.

– Các điểm A, B, C, D gọi là các đỉnh.

– Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh.

2.2. Tứ giác lồi

Định nghĩa tứ giác lồi:

Tứ giác lồi là tứ giác có luôn nằm trong cùng một phần mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

Chú ý: Từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi.

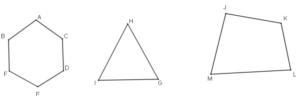
Ví dụ 1. Hình nào trong các hình sau là tứ giác, đó có phải tứ giác lồi không?

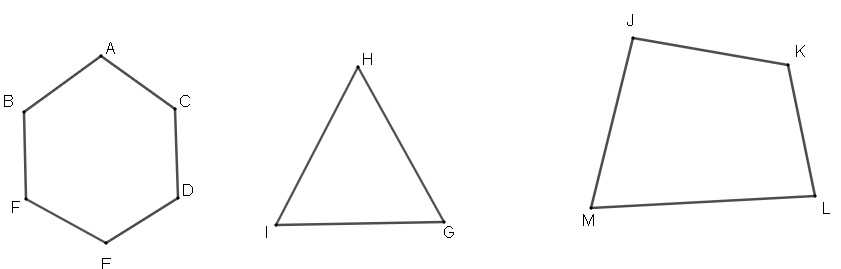
Hướng dẫn giải

–Theo định nghĩa tứ giác, trong các hình trên chỉ có JKLM là tứ giác.

–Theo định nghĩa tứ giác lồi, nếu kẻ một đường thẳng bất kì đi qua hai cạnh của tứ giác JKLM thì đều đảm bảo hai đỉnh thuộc một cạnh còn lại luôn nằm về một phía của đường thẳng đó. Vì vậy tứ giác JKLM là tứ giác lồi.

Cạnh, góc, đường chéo của tứ giác

Trong một tứ giác:

a) Hai cạnh kề nhau là hai cạnh có chung một đỉnh.

b) Hai cạnh kề nhau tạo thành một góc của tứ giác.

c) Hai cạnh đối nhau là hai cạnh không có chung đỉnh nào.

d) Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.

e) Đường chéo của đoạn thẳng nối hai đỉnh với nhau.

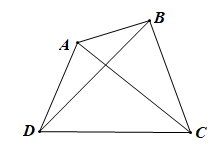
Ví dụ 2. Cho hình vẽ dưới đây:

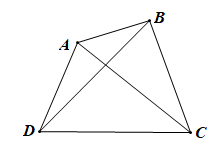
Trong tứ giác ABCD, có:

• BA và BC; AB và AD; CB và CD; DA và DC là các cặp cạnh kề nhau.

• các góc DAB^,ABC^,BCD^,CDA^ . Các cặp góc DAB^ và BCD^ ; ABC^ và CDA^ được gọi là cặp góc đối.

• AB và DC; AD và BC là các cặp cạnh đối nhau.

• Đỉnh A và C; đỉnh B và D là các cặp đỉnh đối nhau.

• AC và BD là hai đường chéo.

2. Tổng các góc của một tứ giác

Định lí:Tổng số đo các góc của một tứ giác bằng 360°.

Ví dụ 3. Tính trong tứ giác ABCD ở hình vẽ sau:

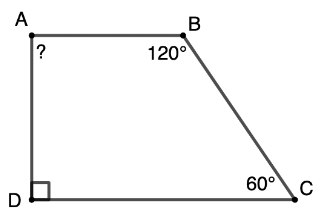
Hướng dẫn giải

Theo định lí tổng các góc của một tứ giác, tứ giác ABCD có: A^+B^+C^+D^=360o

Do đó A^=360o−B^+C^+D^

A^=360o−120o+60o+90o=360o−270o=90o

Vậy A^=90o .

Bài tập Tứ giác

Bài 1. Cho bốn điểm E, F, G, H (hình vẽ).

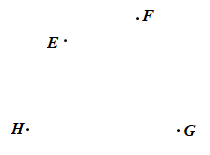
Vẽ một tứ giác có các đỉnh là bốn điểm đã cho và tìm các yếu tố sau:

a) cạnh kề, cạnh đối của cạnh GH.

b) góc đối của EFG^ .

c) hai đường chéo của tứ giác.

Hướng dẫn giải

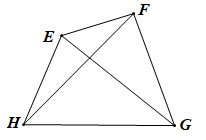
a) Cạnh kề của cạnh GH là cạnh GF; cạnh đối của cạnh GH là cạnh EF.

b) Góc đối của EFG^ là EHG^ .

c) Hai đường chéo của tứ giác là EG và FH.

Bài 2. Tính x trong mỗi hình sau:

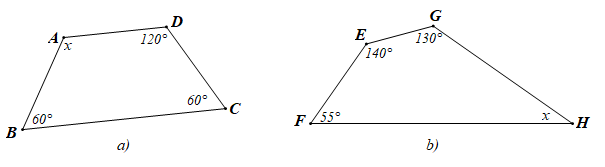
Hướng dẫn giải

a) Theo định lí tổng các góc của một tứ giác, trong tứ giác ABCD có:

A^+B^+C^+D^=360o

Suy ra x=A^=360o−B^+C^+D^

x=360o−60o+60o+120o=360o−240o=120o

Vậy x=120o .

b) Theo định lí tổng các góc của một tứ giác, trong tứ giác EGHF có: E^+G^+H^+F^=360o

Suy ra x=H^=360o−E^+G^+F^

x=360o−140o+130o+55o=360o−325o=35o

Vậy x=35o

Bài3.Tứ giác ABCD có C^=50° ; B^=60° ; A^−B^=40° . Tính số đo các góc A và D.

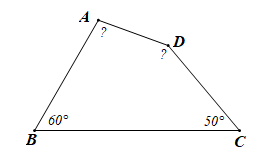
Hướng dẫn giải

Theo giả thiết: A^−B^=40onên A^=40o+B^=40o+60o=100o

Theo định lí tổng các góc của một tứ giác, trong tứ giác ABCD có:

A^+B^+C^+D^=360o

Suy ra D^=360o−B^+C^+A^

D^=360o−60o+50o+100o=360o−210o=150o

Vậy A^=100o;D^=150o

Học tốt Tứ giác

Các bài học để học tốt Tứ giác Toán lớp 8 hay khác:

Xem thêm tóm tắt lý thuyết Toán lớp 8 Chân trời sáng tạo hay khác:

Xem thêm các tài liệu học tốt lớp 8 hay khác:

---