Lý thuyết Tập hợp Q các số hữu tỉ lớp 7 (hay, chi tiết) – Tổng hợp lý thuyết Toán lớp 7 hay, chi tiết giúp học sinh nắm vững kiến thức trọng tâm Toán 7.-Lý thuyết Tập hợp Q các số hữu tỉ lớp 7 (hay, chi tiết)
Lý thuyết Tập hợp Q các số hữu tỉ lớp 7 (hay, chi tiết)
Bài viết Lý thuyết Tập hợp Q các số hữu tỉ lớp 7 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm
Tập hợp Q các số hữu tỉ.
Lý thuyết Tập hợp Q các số hữu tỉ lớp 7 (hay, chi tiết)
1. Số hữu tỉ
• Các phân số bằng nhau là cách viết khác nhau của cùng một số, số đó được gọi là số hữu tỉ.
• Số hữu tỉ là số được viết dưới dạng phân số a/b với a, b ∈ Z và b ≠ 0
• Tập hợp các số hữu tỉ được kí hiệu là Q (x là số hữu tỉ thì ghi là x ∈ Q)
Ví dụ 1:
Ta có thể viết
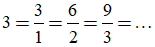
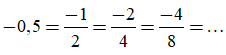
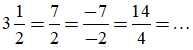
Ví dụ 2:
Các số hữu tỉ ví dụ như:
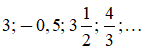
Ví dụ:
Các số hữu tỉ ví dụ như:
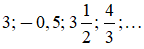
thì kí hiệu như sau:
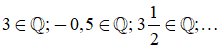
2. Biểu diễn các số hữu tỉ trên trục số
Để biểu diễn số hữu tỉ a/b (a,b ∈ Z; b > 0) trên trục số ta làm như sau:
• Chia đoạn đơn vị [0;1] trên trục số thành b phần bằng nhau, mỗi phần là 1/b được gọi là đơn vị mới .
• Nếu a > 0 thì phân số a/b được biểu diễn bằng một điểm nằm bên phải điểm O và cách điểm O một đoạn bằng a lần đơn vị mới .
• Nếu a < 0 thì phân số a/b được biểu diễn bằng một điểm nằm bên trái điểm O và cách điểm O một đoạn bằng |a| lần đơn vị mới .
3. So sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ x, y ta thường làm như sau:
• Viết x, y dưới dạng hai phân số có cùng mẫu dương
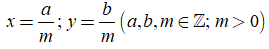
• So sánh hai số nguyên a và b
+ Nếu a < b thì x < y
+ Nếu a = b thì x = y
+ Nếu a > b thì x > y
• Trên trục số nếu x < y thì điểm x nằm bên trái điểm y
• Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương.
• Số hữu tỉ nhỏ hơn 0 được gọc là số hữu tỉ âm.
• Số 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.
Nhận xét:
+ Số hữu tỉ a/b là số hữu tỉ dương (a/b > 0) thì a, b cùng dấu.
+ Số hữu tỉ a/b là số hữu tỉ âm (a/b < 0) thì a, b trái dấu.
+ Ta có:
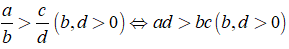
Ví dụ: So sánh hai số hữu tỉ
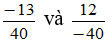
Ta có:
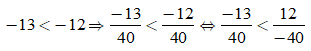
Bài 1: Với ba chữ số 1, hãy biểu diễn số hữu tỉ âm lớn nhất và số hữu tỉ âm nhỏ nhất.
Lời giải:
+ Số hữu tỉ âm nhỏ nhất là -111
+ Số hữu tỉ âm lớn nhất là -1/11
Bài 2: So sánh các số hữu tỉ sau bằng cách nhanh nhất
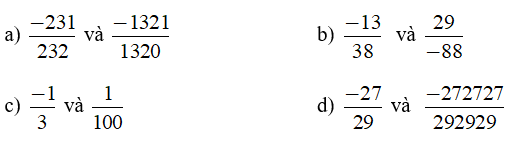
Lời giải:
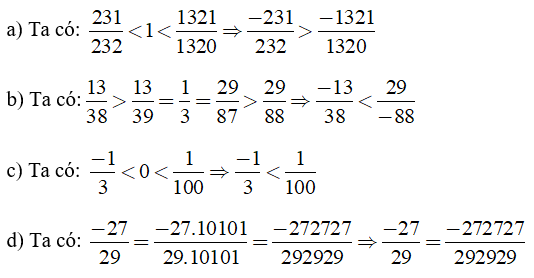
Bài 1. Cho các số sau: 04; -112; 127; -437; -90; -7-9; 0,05; −3,425.
Hãy cho biết số nào là số hữu tỉ, số nào không phải là số hữu tỉ?
Hướng dẫn giải:
Ta có
04=0; -112=-32; 127; -437; -90; -7-9; 0,05=120;-3,425=-34251000.
Vậy các số hữu tỉ là: 04; -112; 127; -437; -7-9; 0,05; −3,425.
Số không phải là số hữu tỉ là: -90 vì có mẫu số là 0.
Bài 2. Điền kí hiệu thích hợp (∈, ∉, ⸦, ⸧, ℕ, ℤ, ℚ) vào ô trống:
a) 6 … ℕ; −4 … ℕ;
b) -23 …ℤ; 3-5… ℚ
c) ℤ … ℕ; ℕ … ℤ … ℚ.
Hướng dẫn giải:
a) 6 ∈ ℕ; −4 ∉ ℕ;
b) -23 ∉ ℤ; 3-5∈ ℚ
c) ℤ ⸧ ℕ; ℕ ⸦ ℤ ⸦ ℚ.
Bài 3. So sánh các số hữu tỉ sau:
a) 27 và 15;
b) -116 và 8-9;
c) 20172016 và 20172018;
d) -249333 và -83111.
Hướng dẫn giải:
a) Ta có: 27=2.57.5=1035 và 15=75.7=735.
Do đó 1035>735⇒27>15.
b) Ta có: -116=-3318 và 8-9=-89=-8.29.2=-1618.
Do đó -3318<-1618⇒-116<8-9.
c) Ta có: 20172016>1 và 20172018<1.
Nên suy ra 20172016>20172018.
d) Ta có: -249333=-83.3111.3=-83111.
Bài 4. Cho số hữu tỉ x=2a-12 với giá trị nào của a thì:
a) x là số dương;
b) x là số âm;
c) x không là số dương cũng không là số âm.
Hướng dẫn giải:
a) Để x là số dương thì 2a-12>0 nên 2a -1 > 0 suy ra x>12.
b) Để x là số âm thì 2a-12<0 nên 2a – 1 < 0 suy ra x<12.
a) Để x không là số dương cũng không là số âm thì 2a-12=0.
nên 2a – 1 = 0 suy ra x=12.
Bài 5. Cho hai số hữu tỉ ab và cd (a, b, c, d ∈ ℤ, b > 0, d > 0). Chứng minh ad < bc khi và chỉ khi ab<cd.
Hướng dẫn giải:
Ta có ad < bc ⇒adbd<bcbd⇒ab<cd
Ngược lại ab<cd⇒ab.bd<cd.bd⇒ad<bc
Vậy ta có điều phải chứng minh.
Bài 6. Cho số hữu tỉ x=3a-24. Với giá trị nào của a thì
a) x là số dương;
b) x là số âm;
c) x không là số dương cũng không là số âm.
Bài 7. So sánh các số hữu tỉ sau:
a) 25 và 14;
b) -95 và 116;
c) 3435 và 3534.
Bài 8. Điền kí hiệu thích hợp (∈, ∉, ⸦, ⸧, ℕ, ℤ, ℚ) vào ô trống:
a) 2 … ℕ; −11 … ℚ;
b) -23… ℚ; 3-5… ℤ
c) ℕ … ℤ; ℚ … ℤ … ℕ.
Bài 9. Cho các số sau: 54;-1125;-12-5;-38;10;-77-99;0,105;-4,25.
Hãy cho biết số nào là số hữu tỉ?
Bài 10. Cho số hữu tỉ x=a-4a(a≠0). Với giá trị nào của a thì x đều là số nguyên?
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 7 có đáp án chi tiết hay khác:
Lời giải bài tập lớp 7 sách mới:

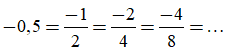
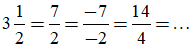

Nội dung được phát triển bởi đội ngũ Meraki Center với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@merakicenter.edu.vn